大电网静态稳定态势评估的大数据融合方法
由于输入数据的高维矩阵X中所含元素均为实数,通过利用酉矩阵U对X的样本协方差矩阵进行处理后可将特征值映射到复平面。样本协方差矩阵X经过奇异化处理后得到等效矩阵Xu=UXX′−−−−√Xu=UXX′[24-25],U为haar矩阵,满足XuXTu=XXTXuXuT=XXT。对该矩阵中元素按照式(7)进行单位化处理,得到标准矩阵Z。
zi=xiN√σ(xi),i=1,2,…,Nzi=xiNσ(xi),i=1,2,…,N(7)
矩阵Z的方差和期望满足E(zi,j)=0,σ2(zi,j)=1/N,此时Z的ESD将收敛于一个圆环,服从于式(8)。
式中c=N/T,根据圆环率,当系统中无事件发生处于稳定状态时,在复平面上,特征值分布在一个外环半径为1,内环半径为(1-c)2/L的圆环之间。
对数据处理后分析结果可视化如图2所示,当系统稳定运行时,所有特征值落在圆环之间,如图2(a)。在此基础上逐渐增加负荷,可以看到特征值分布逐渐靠近圆心,如图2(b)。当负荷增加到一定程度,系统接近崩溃时,特征值的分布更接近圆心,分布范围更广。
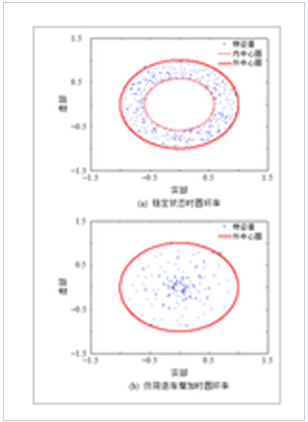
图2系统不同状态的圆环率
通过以上两种不同的极限谱分布函数方法,观察极限谱分布函数的变化规律,评估静态稳定态势的方法可行。
2.3平均谱半径
通过2.2节的分析,可以看出当系统发生事件时,系统的随机性会被破坏,随机矩阵的特征值分布会发生变化,不再符合M-P率和圆环率。特征值的分布随着负荷增长而变化,矩阵的单个特征值由于随机性不能反映这种特性,故引入线性特征值统计量(lineareigenvaluestatistic,LES)用来反映特征值的统计特性,作为评价指标。
引入平均谱半径(meanspectralradius,MSR)进行分析,平均谱半径为复平面上所有特征值距离中心点距离的平均值,是一种线性特征值统计的方法,公式如式(9),其中λ1,λ2,,λi,,λn为矩阵特征值。
rMSR=1N∑i=1N|λi|,i=1,2,…,NrMSR=1N∑i=1N|λi|,i=1,2,…,N(9)
3静态稳定态势评估步骤
根据上述介绍,静态稳定态势评估步骤如下:
1)采集量测数据,根据研究内容确定随机矩阵中数据内容,生成原始数据矩阵。
2)采用实时分离窗技术,确定窗口宽度。分别从原始数据矩阵中取得对应矩阵,对矩阵进行归一化及标准化预处理。
3)计算所取出时间窗口的样本协方差矩阵或者对应的奇异化样本协方差矩阵。
4)采用M-P率求出特征值及对应的谱分布,或采用圆环率求出特征值及对应的圆环。
5)求出平均谱半径。
6)重复步骤3)—6),直到窗口滑动到当前时刻。
7)绘制出平均谱半径趋势图,并对其进行分析,对比当前时刻和历史时刻的平均谱半径。
8)综合以上步骤,评估静态稳定态势,同时检测出异常时刻以及异常状态量。
这一方法间接避免了复杂网络潮流计算和具体临界值求取。
4算例分析
为了研究本文方法的有效性,本文采用IEEE39节点配电网络作为算例,并根据需要对其做了改动。IEEE39节点网络拓扑如图3所示,其中发电机节点10个,变压器节点12个,负荷节点17个。本文进行了两组算例的仿真。
4.1算例1
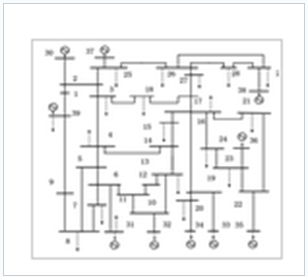
图3IEEE39节点网络拓扑
本算例原始数据是IEEE39节点中17个负荷节点总负荷连续增长,每个负荷节点负荷都发生变化。选取每一状态点的所有节点电压和负荷节点的有功功率构成56维随机矩阵,一共956个采样时刻,其中前200个时刻为系统稳定状态,从第201个时刻开始,总负荷连续增长,取时间窗口TwTw=80,依次对每个滑动时间窗口构成的矩阵按照上文方法进行平均谱半径的计算,结果如图4所示。

图4平均谱半径曲线
从图4中可以看出,由于时间窗口为80,故平均谱半径数值从第80个采样点开始分析,时间窗口中包含历史数据,在稳定时刻平均谱半径曲线平稳,随着总负荷的增加,系统负荷裕度降低,平均谱半径呈下降趋势,系统趋于不稳定状态。
4.2算例2
本算例设置IEEE39节点中第18节点处负荷功率连续增加,其余负荷节点处负荷功率保持不变。一共361个采样时刻,其中前200个采样时刻系统处于稳定状态,从201个采样时刻开始第18节点处的负荷功率开始连续增加。选取每一个采样时刻系统发电机节点、负荷节点处母线电压共27维数据和所有负荷节点有功功率共17维数据构成44维随机矩阵进行分析,选取时间窗口TwTw=80,依照上文介绍方法进行静态稳定性态势评估,采样时刻和平均谱半径曲线如图5所示。
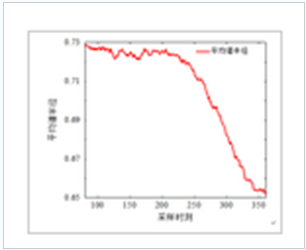
图5平均谱半径曲线
可以看出从第80个采样时刻到第200个采样时刻平均谱半径相对平稳,波动是由于噪声和随机矩阵服从统计规律造成的,若扩大滑动窗口宽度,去噪能力增强,曲线会相对平滑。从第200个采样时刻开始平均谱半径数值呈降低趋势,事实上,总负荷功率在此时间段内为上升趋势。
为寻找何处负荷功率变化对电网产生影响,采用增广矩阵方法,提取电网状态数据与负荷数据之间的相关性,先选取每一个采样时刻系统发电机节点、负荷节点处母线电压共27维数据,在此基础上依次分别选取17个负荷节点处的有功功率扩展到27维,构成54维的随机矩阵进行仿真分析,时间窗口Tw=80,结果如图6所示。
从图中可以看出一共17条曲线,每一条曲线

图6不同负荷的平均谱半径曲线
对应一个负荷节点有功功率与发电机、负荷节点的电压构成的随机矩阵。在第200个采样时刻之前17条曲线平均谱半径值均呈现出平稳的趋势,而后,其中16条平均谱半径值相对平稳,1条曲线的平均谱半径呈现下降趋势。曲线和随机矩阵一一对应,随机矩阵和电网负荷节点一一对应,可以看出第18节点处负荷功率发生了变化。
5结论
本文在分析电力系统实际运行产生的数据基础上,利用随机矩阵的相关理论,提出了一种电网静态稳定态势的评估方法,得出以下结论:
1)随着电网多源广域量测信息平台的完备,本文采用高维随机矩阵模型提出了电网静态稳定态势的表征方法,实现电网各个节点不同的状态量的数据融合。
2)相对于传统的静态稳定态势评估方法,本文方法融合状态量多,数据量相对较大,充分利用电网产生的数据,将数据转化为知识,避免了通过机理建模中各种简化和假设导致分析结果不能充分反映系统实际运行情况的问题,提高了评估的可靠性。
3)本方法将历史数据和当前数据充分应用,基于随机矩阵理论,通过对M-P率或圆环率求得的特征值分析,利用平均谱半径作为评价指标,进行静态稳定态势的评估。
4)通过算例分析计算可以验证该方法的有效性,此外还可以对负荷功率变化节点进行检测,提出的方法可以用来进行负荷薄弱节点判别,需要结合实际数据做进一步分析。
-
2017年云计算市场营收增长24%,达1800亿美元
2018-01-10市场 -
人人称道的云计算,市场发展仍存几大障碍
-
当春运遇上云计算
2018-01-10当春运遇上云计算
-
2017年云计算市场营收增长24%,达1800亿美元
2018-01-10市场 -
人人称道的云计算,市场发展仍存几大障碍
-
当春运遇上云计算
2018-01-10当春运遇上云计算