大电网静态稳定态势评估的大数据融合方法
近年来,新一代智能电网调度技术支持系统实现了电网静态和动态信息的采集功能,随着广域测量系统(wide area measurement system,WAMS)在工程中广泛应用,WAMS系统可在时空统一角度且具有足够的精度和速度测量电网真实运行状态信息,为大电网稳定态势评估带来新的契机。
静态稳定态势分析通常采用模型仿真,但是每次仿真分析前需要确定全部数学模型,参数及仿真场景,故计算量大,存在维数灾难,且难以计及非常规数据的影响,仍需要花费大量时间和精力。模型法分析结果的准确性取决于机理模型的准确性,建模过程中的各种简化和假设使模型法的分析结果不能充分反映电网实际运行状况。此外,随着电网规模扩大、电网有些区域会接近输电极限,加之大规模间歇性新能源(renewable energy systems,RES)并网发电大大增加了电力生产的不确定性和电网运行困难;大规模电动汽车(electric vehicle,EV)充放电又增加了电力负荷的随机性,这些各个环节不确定因素及其交互影响使得电网稳定行为更为复杂,传统研究假设条件可能会不成立。
大数据技术近年来受到广泛关注,它对大量多源数据进行高速捕捉、发现和分析,利用经济的方法提取有价值的技术体系或架构。广义上讲,大数据不仅指所涉及的数据,还包含了对这些数据进行处理和分析的理论、方法和技术。随着我国智能电网建设的不断推进和深入,电网量测体系积累了大量的数据,这就使得大数据分析挖掘技术在静态稳定态势评估具有可行性。
目前,电网存在各种类型的大量仿真或实测数据,启发人们思考如何用数据分析取代机理建模,从而提出了数据驱动模式。然而,几乎所有关于大数据的论文都会强调不同类型数据之间的融合,但却鲜有讨论如何融合。
针对以上问题,本文提出了基于随机矩阵理论的静态稳定态势评估方法。随机矩阵理论作为一种普适性的大数据分析方法,无需详细物理模型,可综合考虑历史数据和实时数据,具有从高维角度认识复杂系统等优点。随机矩阵是对复杂网络进行统计分析的重要数据理论之一,通过对复杂系统的能谱和本征态进行统计分析,揭示数据中整体的行为特征,可以从宏观上对复杂系统的性质进行研究分析。随机理论是近年来的研究热点之一,在量子物理、金融工程、医疗等多个领域发挥了重要作用。文献[8]首次将随机矩阵理论引入电力系统,提出一种全新的、通用的大数据分析架构,将其应用于电力系统异常发现;文献提出一种基于随机矩阵理论的配电网运行状态相关性分析方法;文献提出基于高维随机矩阵描述的WAMS量测大数据建模与分析方法;文献提出一种基于高维随机矩阵大数据分析模型的输变电设备关键性能评估方法;文献提出一种随机矩阵在全球能源互联网中的应用框架。然而,大数据技术在电力系统中的应用鲜有涉及如何对静态稳定态势进行评估的介绍。高维随机矩阵理论作为新兴的大数据分析方法,能将各类数据集成到高维矩阵中,从概率和统计角度研究矩阵的特性和数据分布情况。
本文提出了一种电网静态稳定态势评估的大数据融合方法,利用历史数据和实时数据建立了随机矩阵模型。在此基础上,提出了两种基于随机矩阵理论的极限谱分布函数,用来研究矩阵特性和数据分布情况。进而,利用平均谱半径实现静态稳定态势评估。最后,利用IEEE39节点系统算例仿真,验证了所提方法的有效性。
1大数据融合方法
1.1基于随机矩阵理论的大数据融合方法
电力系统实际运行中,发生稳定破坏性故障相对罕见,导致实测数据缺乏失稳数据,难以进行数据挖掘,通常采用仿真计算来获得样本。连续潮流法是电网静态(电压)稳定分析的有效工具,可用于模拟实际电网中发电负荷区域性增长的远景和规划[17-18]。本文进行分析挖掘的数据采用基于负荷增长的连续潮流法(ContinuationPowerFlow,CPF)进行仿真得到大量的样本数据;由于在数据采集和传输过程中会产生随机噪声,电力系统存在小幅度随机扰动。因此,本文在连续潮流仿真数据基础上添加高斯白噪声,以此数据来模拟电网实际运行获得的数据。
随机矩阵理论中渐进收敛性要求矩阵的维数趋近无穷,在处理实际工程问题时,当维数从几十到几百时,也能观察到相当精确的渐进收敛结果[15]。在矩阵构造时,对行列元素通过调整来获得最优的行列比值。
对于电力网络,选择nn个节点的量测数据作为空间样本,每个节点有kk个状态变量,构成NN个变量,其中N=n×k。
在采样时刻titi,每个节点的量测数据可以构成一个列向量:
x(ti)=[x1,x2,⋯,xN]Tx(ti)=[x1,x2,⋯,xN]T(1)
将每个节点采样时刻的量测数据按照时间序列排序,可形成如下矩阵:
XN×T=[x(t1),x(t2),⋯,x(ti),⋯]∈CN×TXN×T=[x(t1),x(t2),⋯,x(ti),⋯]∈CN×T(2)
该矩阵即为大数据分析的数据源,这些数据按照时间顺序采样,不同节点的电气特征量具有空间特性,将两者结合起来则构成具有时空特性的数据源。
1.2静态稳定态势评估的输入数据
电网的运行状态由多种状态变量表征,比如电网各个节点的电压和相角、发电机注入有功功率和无功功率、负荷有功功率和无功功率、支路电流等。电网中各元件间的拓扑关系及相互作用力必然蕴含于广域时空量测信息中。此外,电网的运行状态还受到各种电气因素和非电气因素的影响。电气因素包括分布式电源出力、各类故障和扰动等;非电气因素包括温度、湿度、风速等气候因素和社会经济因素等。在大数据分析时,根据具体的研究目的和数据资源选取量测数据进行数据源随机矩阵的构建。
在采样时,由于不同数据的采样频率可能不同,可以认为采样频率低的数据类型在采样间隔内数值相等。在矩阵分析时,要将所有元素进行标准化处理,其目的是去量纲化和数值归一化,从而使得各个指标具有可比性。
在研究静态电压稳定性时,由于电压失稳是负荷驱动的,侧重研究负荷和电压数据,电压稳定性问题就是负荷的稳定性问题。故而本文在研究静态稳定态势评估时,选取每个节点的节点电压数据和所有负荷节点的有功功率数据构造矩阵。为了实现数据的实时分析,采用文献[13]中提出的实时分离窗技术,该技术可以从数据源中获取当前时刻和历史时刻的采样量测数据,实时分离窗的宽度为Tw,在采样时刻ti,获得的数据矩阵为:
XN×Tw(ti)=[x(ti−Tw+1),x(ti−Tw+2),⋯,x(ti)]XN×Tw(ti)=[x(ti−Tw+1),x(ti−Tw+2),⋯,x(ti)](3)
该技术也可以对噪声数据进行平滑处理。
2随机矩阵理论基本原理
2.1随机矩阵理论
随机矩阵理论有两个基本概念,经验谱分布函数和极限谱分布函数。对于任意特征值为实数的n×nn×n维随机矩阵A,称函数
FA(x)=1n∑i=1nI(λAi≤x)FA(x)=1n∑i=1nI(λiA≤x)(4)
为矩阵A的经验谱分布函数(empiricalspectrumdistribution,ESD),这里λAiλiA为矩阵A的特征根,i=1,⋯,ni=1,⋯,n,I(•)表示指示性函数。我们把经验谱分布函数的极限称为极限谱分布函数。经验谱分布函数是随机的,但通常极限谱分布函数是非随机的,如圆率,半圆率、M-P率(Marchenko-PaturLaw)和圆环率。
对于高维数据源X矩阵,其样本协方差阵如下式所示:
Sn=1n(∑i=1nxix′i)=1nXX′Sn=1n(∑i=1nxix′i)=1nXX′(5)
可求得其经验谱分布函数FSn(x)FSn(x),通过对其进行Stieltjes变换[19-21],利用Stieltjes变换法,可以把对随机矩阵经验谱分布函数研究转换为对随机矩阵逆的迹的研究,由此求得极限谱分布函数。
2.2M-P率和圆环率
利用随机矩阵理论评估静态稳定态势重点,是根据极限谱分布函数的变化规律来评估静态稳定裕度。下文将介绍两种极限谱分布函数M-P率和圆环率[12,22-23]。
采用M-P率观测谱分布,M-P率其极限谱密度如式(6)。
式中,a=σ2(1−c√)2a=σ2(1−c)2,b=σ2(1+c√)2b=σ2(1+c)2这里c为维数与样本量的比值,σ2σ2为刻度参数,σ2=1σ2=1。通过对连续潮流输入数据预处理后,应用实时分离窗技术,选取不同状态可以看出样本协方差谱分布直方图和M-P率曲线如图1所示。
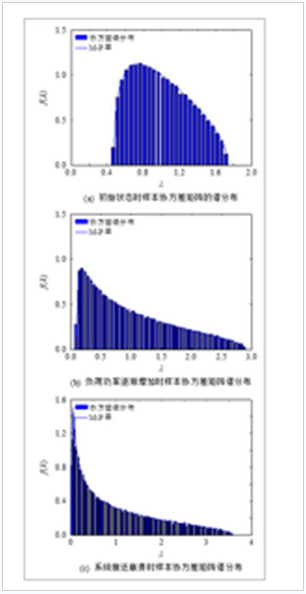
图1样本协方差矩阵谱分布
图中展示了随着负荷的不断增长,样本协方差矩阵谱分布直方图变窄变长。可以明显看出电力系统发生了变化。
由于输入数据的高维矩阵X中所含元素均为实数,通过利用酉矩阵U对X的样本协方差矩阵进行处理后可将特征值映射到复平面。样本协方差矩阵X经过奇异化处理后得到等效矩阵Xu=UXX′−−−−√Xu=UXX′[24-25],U为haar矩阵,满足XuXTu=XXTXuXuT=XXT。对该矩
-
2017年云计算市场营收增长24%,达1800亿美元
2018-01-10市场 -
人人称道的云计算,市场发展仍存几大障碍
-
当春运遇上云计算
2018-01-10当春运遇上云计算
-
2017年云计算市场营收增长24%,达1800亿美元
2018-01-10市场 -
人人称道的云计算,市场发展仍存几大障碍
-
当春运遇上云计算
2018-01-10当春运遇上云计算