互联网环境下智慧售电关键技术——评估技术
当电力消费置于互联网环境下,最大的变革在于用电行为、交易、过程、电力调度及分布能源生产等电能的全生命周期均建立在互联网虚拟空间和基于数据驱动的过程建模、分析及优化。因此,“互联网+智慧售电”的实现即是一个数据获取、传输、业务表达与价值发现过程。其中数据获取主要依靠智能用电物联网系统,通过连接各种用电器、分布能源和检测模块,获取各种基础数据信息;数据传输主要依靠近距离通信、公共通信网络等组成异构融合的数据传输网络,将数据汇聚至云计算平台;数据的业务表达和价值发现主要依靠大数据组织、可视化、挖掘等技术完成数据驱动的电力消费过程。
5.1.4智能用电物联网节点通信重要性评估技术
电力物联网已经成为电网的重要组成部分,承载的业务量也变得越来越多,增长速度惊人,尤其是更多新能源设备、智能控制设备、智能家电等终端的接入使得电力物联网通信网络规模的不断扩大,对安全性、可靠性评估也变得越来越重要。而电力通信网中的重要节点在很大程度上决定了电力通信网的稳定性和安全性,对重要节点的重点维护和管理成为电力通信网的一个重要任务。
电力物联网通信网中的重要节点决定了网络的稳定性和安全性,电力通信网中节点的重要性表明了该节点在可能的故障情况下对网络性能的影响,使用定量的方法来对网络节点进行评估已经成为电力通究的热点。目前国内外对电力通信网节点的重要性评估主要存在下面一些方法:
(1)利用节点的度作为节点重要性的指标。该方法中某节点的的链接的边越多,那么该节点的重要性就越大。
(2)基于节点删除的评价。该方法通过删除某个节点,看网络的连通性的变化来分析节点的重要性。
(3)基于节点的介数的评价,如果该节点的介数越大那么该节点越重要。
(4)通过节点紧密度来对节点进行评价,紧密度越大则节点的重要性越强。
目前的电力通信网节点重要性评估主要采用以上几种方法,但是以上的方法都具有一些缺陷:以节点的度作为评价指标存在一定的片面性,如桥节点的度虽然不大,但重要性却很强;基于节点删除的方如果删除的是末梢节点,那么就不能实现节点重要性的客观评估;另外,由于介数和紧密度是对节点在全局的影响的定义,因此基于介数紧密度的方法也存在着一些不合理性。
目前,有关电力物联网通信网节点重要性评估的工作基本上都是以单一连接权值为主,还没有将距离和带宽都考虑进评估模型的。而且,以往的电力通信网的节点重要性评估往往只利用单个的评价指标,而没有有效的综合多种评价指标,并且很多方法只针对网络结构本身,而忽略了网络的连接权重。针对目前电力通信网评估存在的各种问题,利用网络带宽和距离作为加权,通过多种评价指标的综合来对节点的重要性进行评。由于采用多指标的方式进行节点重要性的评估分类,并且这种分类是一种无监督的分类。日前,针对电力通信网节点重要性评估的无监督分类主要为K- means方法。 k-means方法为无监督分类中的主要传统方法,但是因为该方法基于距离,故结果是圆形的聚类形状,并不能很好地对复杂特征的融合进行分类。针对该问题,采用了一种叫做快速密度聚类的方法,该方法发表在2014年的 Science期刊上,该方法不仅利用距离作为分类的度量,还利用密度作为分类的指标,有效解决了k-means方法的不足。在加权网络的基础上,基于快速密度聚类的方法,采用节点度、节点紧密度以及节点的介数作为评价指标,对电力通信网的节点重要性进行评估。利用某省的实际电网通信数据进行检验,验证了该方法在电力通信网中的实用性。
1.节点重要性相关指标分析
节点数为n,边数为m的通信网有权网络数学模型可以用一个加权矩阵来描述,即
 (5-1)
(5-1)
边权邻接矩阵的矩阵元为WGij=Bij,如果节点和节点j之间有连接;WGij。=∞,如果节点i和节点j之间没有连接。其中,WGij、Bij为节点与节点之间线路的权值。边权代表节点间相互作用的强度或难易程度。如果节点之间的距离作为权值,权值越大表示两点间的距离越大,作用越弱。如果节点之间的带宽作为权值,则权值越大作用越大。本书中将距离和带宽的权值进行归一化整合,距离和带宽的权值各为50%。
网络中节点的重要性不但与节点本身的度有一定关系,还与节点的邻居节点的度大小、节点的紧密度、节点的介数存在一定的关联,这指标体现了节点的影响力。节点的影响力包括直接影响力和间接影力,直接影响力反映节点本身影响其他节点的能力,如节点的度。同影响力反映节点通过网络对其他节点施加影响的能力,如节点紧密度介数。利用节点的度、节点的紧密度、节点的介数作为节点重要性的价指标。
节点的度:节点i的度数k是指与该节点直接连接的边数,反映的声是一个节点对于网络中其他节点的直接影响力。具有n个节点的网络中,节点的度不会超过n-1。通常情况下,加权后节点i的强度Si定义为
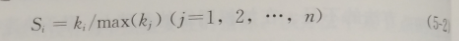
节点的紧密度:紧密度指标C用于刻画网络中的节点通过网络到其他节点的难易程度,反映节点的间接影响力。其值定义为该节点到所有其他节点的距离之和的倒数。具有n个节点的网络中,节点到达所有其他节点的距离之和不会小于n-1,则归一化的紧密度指标Ci为
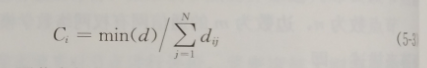
对于加权网络,两节点间的距离dij一般定义为连接两节点间的最短路径上边的权值之和。
介数指选取复杂网络理论中合适的静态几何参量进行网络拓扑脆弱性的计算。每个节点的介数用参数bi表示,反映节点在网络连通中的重要程度。bi也反映了节点拓扑脆弱性,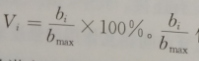 代表节点在整个网络中的脆弱程度,代表节点相对拓扑的重要度,测度了故造成的潜在影响程度,能够直接找到最脆弱点。
代表节点在整个网络中的脆弱程度,代表节点相对拓扑的重要度,测度了故造成的潜在影响程度,能够直接找到最脆弱点。
2.快迷密度聚类
针对目前非监督聚类存在的一些问题,采用快速密度聚类的方法进行电力通信网的节点重要性评估分类。快速密度聚类算法的核心思想是:类簇中心被具有较低局部密度的邻居点包围,且与具有更高密度的任何点有相对较大的距离。基于这种思想,对于任意数据点i,需要计算两个量:局部密度值pi以及点i到具有更高局部密度点的距离δi。Pi 和δi的值都与数据点之间的距离dij有关(dij代表点i和点j之间的距离,文中用欧式距离表示)。任意数据点i的局部密度Pi如下定义
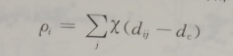 (5-4)
(5-4)
其中dc是截断距离,如果dij-dc<0,那么x(dij-dc)=1,如果dij-dc≥0,那么就有X(dij-dc)=0。数据点i的局部密度Pi本质上为数据点i距离为dc内的点的个数。实验表明分类结果对dc的大小选择具有很高的鲁棒性,及dc的大小对分类结果影响不大。算法中,对于dc的选择规则为:使得点的平均邻居数大概是数据集中点的总数的1%~2%。点i到具有更高局部密度点的距离δi定义为
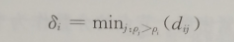 (5-5)
(5-5)
在算法中具有高B和相对较高的,的点可被认为是类簇中心,类簇中心找到后,剩余的每个点被归属到它的有更高密度的最近邻所属类簇。类簇分配只需一步即可完成,不像其他算法要对目标函数进行选代优化。图5-10的简单示例展示了算法的核心思想,图5-10(a)为聚类中心的寻找,图5-10(b)为样本点的聚类。
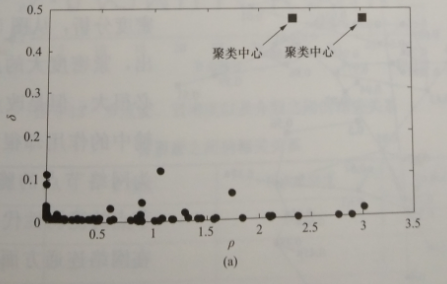
图5-10算法实例展示(一)
(a)聚类中心决策图
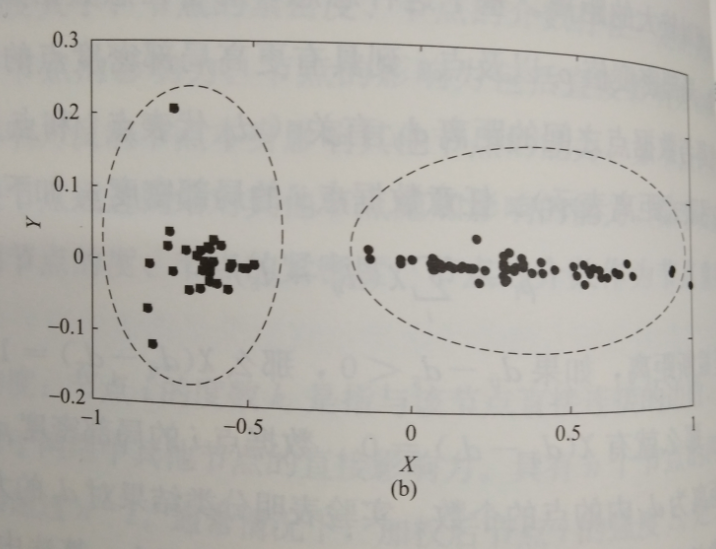
图5-10算法实例展示(二)
(b)二维聚类图
3.节点重要性分类结果
利用节点度、节点紧密度、节点的介数作为节点重要性的评价指标。节点的度的大小非常的直观,反映了节点本身影响其他节点的能力力。一般情况下,度越大的节点重要性越大,但是对于某些桥节点来说却不正确。间接影响力反映节点通过网络对其他节点施加影响的能力,如节点的紧密度和介数
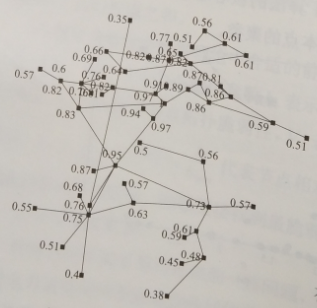
图5-11 节点紧密度分析图
图5-11是网络节点时密度分析从图5-11可以看出,紧密度大的点,其度未必很大,但是改点在数据传输中的作用很大。图5-12为网络节点的脆弱性分析,节点的脆弱性代表了该节点在网络连通方面的能力,如过联通能力强,那么该节点遭到损毁后对网络的影响就越大,即认为脆弱性强。从图5-12可以看出,节点的脆弱性并不和节点的度分布和紧密度呈完全的正相关关系。
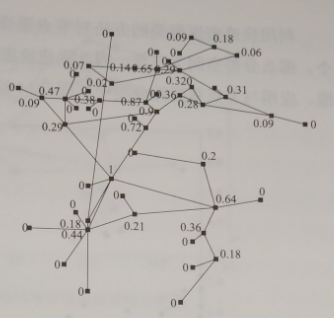
图5-12 节点脆弱性分析
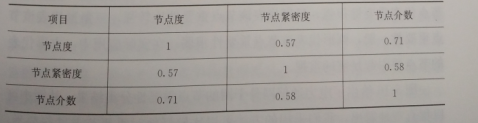
图5-13给出了各种因素的分布,表5-3给出了这三种要素之间的相关性。从图5-13中和表5-3中可以看出,这三种因素之间并不完全是正相关的关系。因此在节点重要性的度量上,需要综合考虑这三种因素。
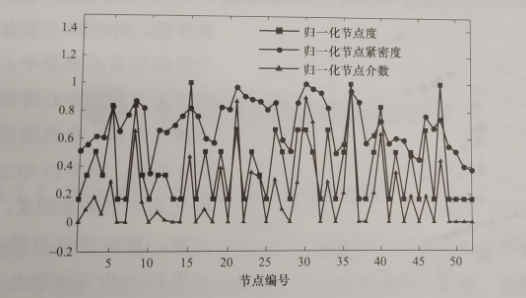
图5-13节点度、紧密度以及介数之间的相关关系
表5-3 各要素之间的相关关系
利用快速密度聚类的方法对节点重要性进行评估。文中的要素为3个,那么分类空间为三维。因此将快速密度聚类的方法由二维推广至三维,应用与节点重要性分类中,图5-14给出了基于三种因素的聚类中心
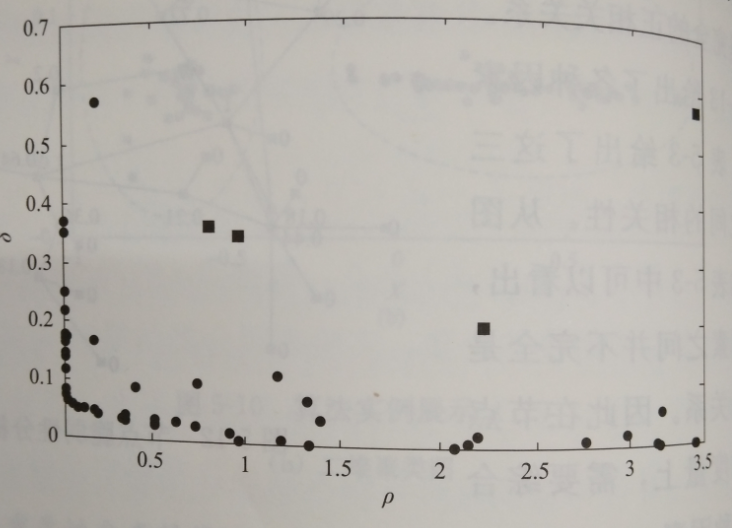
图5-14基于快速密度聚类的聚类中心选择图
选择图,图中的4个方块即为我们所需的聚类中心,按照这4个聚类中心将所有节点进行聚类,聚类结果如5-14所示。
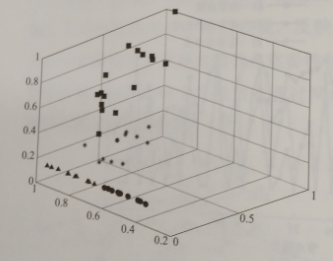
图5-15 节点的重要性聚类分布图
图5-15中三个维度代表三个聚类因素,即节点度、紧密度以及脆弱性。从图5-15中可以看出,该方法可以很好地将节点进行重要性分类。图5-15中方形节点代表重要性很强,星形代表该节点重要性比较强,三角形代表该节点重要性一般,圆形代表该节点重要性很弱。在实际应用中,方形代表的节点要引起足够的重视。
图5-16给出了电力通信网骨干网的节点重要性分类结果,从图中可以很直观地看出,我们采用的方法可以比较好地对重要节点进行分类。
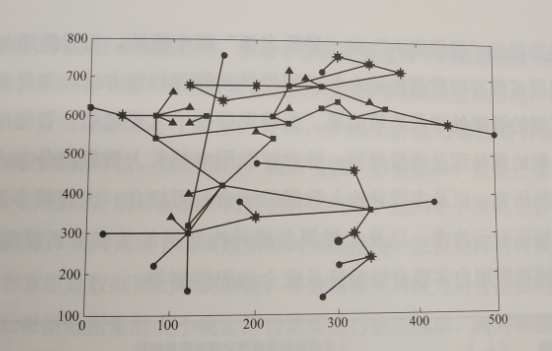
图5-16 电力通信网节点的重要性分类图
对于重要性一般的节点和重要性比较弱的节点来说,由于文中采用了距离和带宽作为权值的一部分,因此一般重要性节点在距离和带宽的加权值比重要性比较弱的节点大。这也就是图5-16中一般重要性节点和重要性比较弱的节点的区别。

责任编辑:电力交易小郭