混合聚类分析算法在发电设备故障模式识别中的应用
0 引言
大型火电厂主、辅机数量较多,结构复杂,其作用是完成从热能到机械能再到电能的转换过程。设备与设备之间的耦合性、系统的复杂性等因素决定了火电厂是一个高故障率和故障危害性很大的生产场所,这些故障都将造成重大的经济损失和社会后果,因此应用设备故障预警及状态监测技术,掌握关键设备的正常运行状态,及时发现易损部件的工况恶化趋势,及时进行维护和检修,对提高设备的可靠性和安全性十分必要[1-5]。
目前,发电设备预警和预知维修的关键技术主要有状态监测技术、故障诊断与预测技术和维修分析与决策,而故障模式识别是这些技术的基础。本文采用K-means算法与基于EM(期望最大)的高斯混合模型(Gaussian Mixture Model,GMM)算法相结合的聚类分析算法进行故障模式识别,实践结果证明该算法能够很好地用于发电设备智能诊断预测。
1 算法介绍
1.1 K-means算法
K-means算法,也被称为K-平均或K-均值算法,是一种得到广泛应用的聚类分析方法[6]。该算法的主要思想是:将各个聚类子集内所有数据样本的均值作为该聚类的代表点,通过迭代的方法逐次更新各聚类中心的值,把数据集划分为不同的类别,最终目标是使评价聚类性能准则的函数达到最优,使生成的每个聚类(簇)内紧凑,类间独立[7-10]。
假设要把样本集X={x1, x2, x3,…, xn}分为K个类别,算法的过程描述如下:
算法:K-means算法,划分并计算基于簇中对象的平均值;
输入:簇的数目
输出:
算法步骤:
1)为每个聚类确定一个初始聚类中心,形成K个初始聚类中心;
2)将样本集中的样本按照最小距离原则分配到最邻近的聚类;
3)利用每个聚类中的样本均值作为新的聚类中心;
4)重复步骤2和步骤3,直到聚类不再变化;
5)迭代结束,得到K个聚类。
K-means算法的优点是算法快速、简单,对大数据集有较高的效率并且是可伸缩的。缺点是需要根据初始聚类中心来确定一个初始划分,然后对初始划分进行优化。在K-means 算法中,多维空间相似性度量基于欧氏距离进行计算,并不能准确反映多维空间点中的相似情况。
1.2 高斯混合模型(GMM)
1.2.1 多维空间单高斯模型(SGM)
假设有一组在多维空间(假设维度为D)的点Xi,i=1,2,…,n,若这些点的分布近似椭球状,则可以用高斯密度函数g(X,μ,Σ)来描述产生这些点的密度函数:
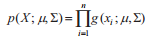
由于xi为己知点,可通过p(X;μ,Σ)来求解μ和Σ。这类问题通常以极大似然估计的方法来进行求解,即在p(X;μ,Σ)为最大值条件下(样本点xi已经发生,故可认为p(X;μ,Σ)样本xi发生的概率最大),求得μ和Σ。根据极值理论,可以通过对μ和Σ分别求导的方式求解。
1.2.2 高斯混合模型(GMM)
SGM样本点的分布为椭球状。而实际中,大部分样本点分布不可能是或近似椭球状,因此引用了高斯混合模型(GMM)。GMM是一种常用的描述混合密度函数分布的模型,可视为多个高斯分布以一定比例混合而成[11-14],GMM模型可描述为:
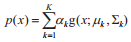
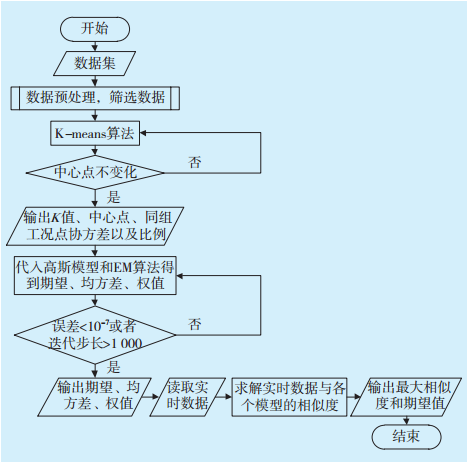
Fig.1 Solution program
基于K-means与GMM结合的聚类分析算法描述如下:
1)引用初始K个高斯混合模型,其初始参数为A0、Mu0、Σ0;
2)在第1次迭代中,通过最大期望算法得到A1、Mu1、Σ1;
3)将更新后的高斯模型进行第2次迭代,得到A2、Mu2、Σ2;
4)进行多次迭代后,值变化达到残差设定值,则迭代结束,得到最终A、Mu以及Σn。
2.2 模型相似度算法详解
在得到高斯混合模型的数学求解结果后,计算机基于EM算法不断求解和迭代可以得到GMM各个模型的参数μ和Σ。在现场得到的实时数据将与GMM中的模型期望值进行相似度比较,相似度最高的期望值将作为实时数据的期望值。
对于2个D维数据对象X={x1, x2,…, xd}和Y={y1, y2,…, yd},相似度计算方法如下:
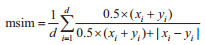
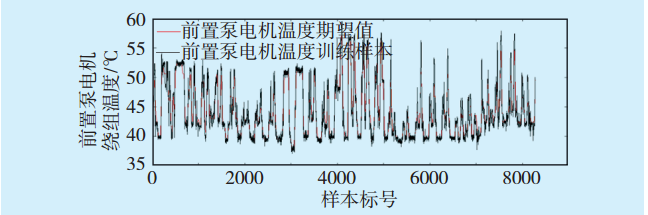 图2 前置泵电机温度训练样本与期望值趋势图Fig.2 Training sample and expected trend of front pump motor temperature
图2 前置泵电机温度训练样本与期望值趋势图Fig.2 Training sample and expected trend of front pump motor temperature
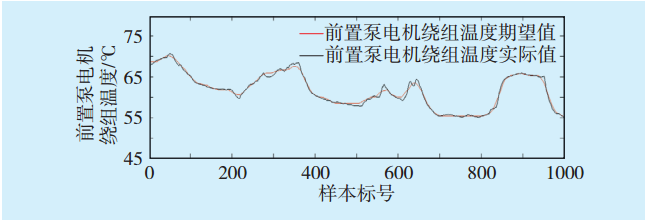 图3 前置泵电机温度实时数据与期望值趋势图Fig.3 Real - time data and expectation trend of front pump motor temperature
图3 前置泵电机温度实时数据与期望值趋势图Fig.3 Real - time data and expectation trend of front pump motor temperature
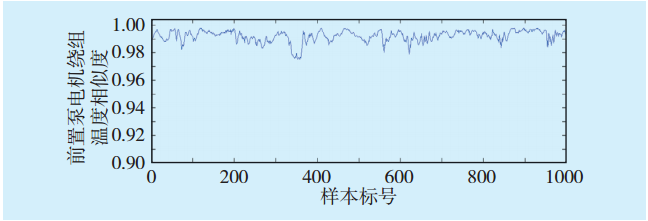 图4 前置泵电机温度相似度趋势图Fig.4 Similarity trend of front pump motor temperature
图4 前置泵电机温度相似度趋势图Fig.4 Similarity trend of front pump motor temperature
从实例可以得出,采用K-means(K均值)与基于EM的GMM算法相结合的聚类分析算法能够对发电设备故障模式进行提取,并以此作为故障模式识别的依据,对于1 000个样本的验证结果,经检验后发现其与实际情况基本吻合。
4 结语
本文针对火力发电机组发电设备故障预警的难题,研究了K-means与GMM结合的聚类分析算法,应用 K-means初始化构建混合高斯模型,使用 EM 算法进行参数估测,并建立了完整的分类模型,验证了该数据挖掘技术在故障诊断中应用的可行性,为发电设备的预警和预知维修奠定了基础。

责任编辑:售电衡衡
-
权威发布 | 新能源汽车产业顶层设计落地:鼓励“光储充放”,有序推进氢燃料供给体系建设
2020-11-03新能源,汽车,产业,设计 -
中国自主研制的“人造太阳”重力支撑设备正式启运
2020-09-14核聚变,ITER,核电 -
探索 | 既耗能又可供能的数据中心 打造融合型综合能源系统
2020-06-16综合能源服务,新能源消纳,能源互联网
-
新基建助推 数据中心建设将迎爆发期
2020-06-16数据中心,能源互联网,电力新基建 -
泛在电力物联网建设下看电网企业数据变现之路
2019-11-12泛在电力物联网 -
泛在电力物联网建设典型实践案例
2019-10-15泛在电力物联网案例
-
权威发布 | 新能源汽车产业顶层设计落地:鼓励“光储充放”,有序推进氢燃料供给体系建设
2020-11-03新能源,汽车,产业,设计 -
中国自主研制的“人造太阳”重力支撑设备正式启运
2020-09-14核聚变,ITER,核电 -
能源革命和电改政策红利将长期助力储能行业发展
-
探索 | 既耗能又可供能的数据中心 打造融合型综合能源系统
2020-06-16综合能源服务,新能源消纳,能源互联网 -
5G新基建助力智能电网发展
2020-06-125G,智能电网,配电网 -
从智能电网到智能城市