电力通信大数据并行化聚类算法研究
确度均高于k-medoids并行化算法和DBSCAN并行化算法,并且在处理较大数量级的数据集时,本文算法准确度更占优势。不同数据集上各算法的执行时间如图2。
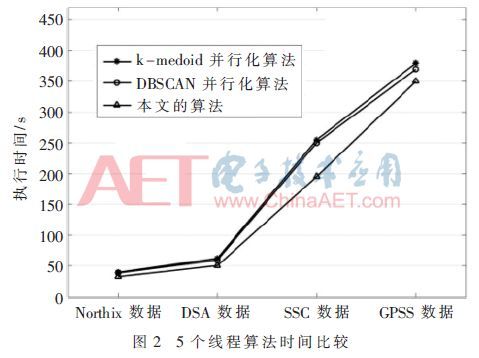
根据图2,随着数据量的增大,三种算法执行效率差异逐渐增大,本文算法性能明显优于k-medoids并行性算法和DBSCAN并行算法。接着对三个算法使用7个线程时的执行时间进行比较,如图3所示。
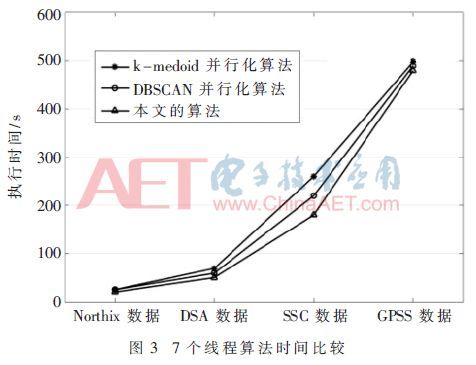
从图3中可以看出,使用7个线程在1 000、5 000、10 000数据级时,本文算法执行时间明显优于其他两个算法。
3.3 实验小结
仿真实验可知,在同一线程数时,本文算法比对比算法聚类准确率高,执行时间短;在线程数增加时,本文算法执行时间显著降低;随着数据量的增长,本文算法在保证更高准确度的基础上,执行时间优势逐渐凸显。
4 结论
本文针对电力通信数据的聚类处理问题,提出基于密度的聚类思想对k-medoids算法初始点的选取策略进行优化,并利用MapReduce编程框架实现了算法的并行化处理。通过仿真实验表明本文提出的优化算法可行有效,并具有较好的执行效率。在接下来的研究中可以考虑线程数小于聚类数时的优化分配策略,进一步提高算法性能。
参考文献
[1] 蔡永强,陈平华,李惠.基于云计算平台的并行DBSCAN算法[J].广东工业大学学报,2016,33(1):51-56.
[2] PARK H S,JUN C H.A simple and fast algorithm for k-medoids clustering[J].Expert System with Applications,2009,36(2):3336-3341.
[3] 赵烨,黄泽君.蚁群K-medoids融合的聚类算法[J].电子测量与仪器学报,2012,26(9):800-804.
[4] 马菁,谢娟英.基于粒计算的k-medoids聚类算法[J].计算机应用,2012,32(7):1973-1977.
[5] 吴景岚,朱文兴.基于k中心点的迭代局部搜索聚类算法[J].计算机研究与发展,2004,41(Z):246-252.
[6] Jiang Yaobin,Zhang Jiongmin.Parallel k-medoids clustering algorithm based on Hadoop[C].Proceedings of the IEEE International Conference on Software Engineering and Service Sciences,2014:649-651.
[7] 孙胜,王元珍.基于核的自适应k-medoid聚类[J].计算机工程与设计,2009,30(3):674-677.
[8] 马晓慧.一种改进的可并行的K-medoids聚类算法[J].智能计算机与应用,2015:874-876.
作者信息:
曾 瑛,李星南,刘新展
(广东电网公司 广东电网电力调度控制中心,广东 广州510600)

责任编辑:售电衡衡