微电网运营商提供无功辅助服务下各市场主体的利益分配
摘要:随着售电侧市场改革的不断深入,研究多个微电网运营商参与下的配电侧市场交易和竞价机制具有重要意义。针对该问题,提出了一种双层优化
2 完全信息博弈下的双层优化方法
针对图1所示的配电侧电力市场,微电网运营商和批发市场以及微电网运营商之间通过竞价竞争中标量,任何报价过高或者过低的一方都可能导致自身利益的损失;另一方面,DSO根据各售电方的报价,综合考虑系统的潮流分布和运行约束,确定购电成本最小的经济调度方案。因此,式(1)—(11)可以描述成一个双层优化问题:底层优化实现DSO对市场的清算,其中目标函数、等式约束和不等式约束大部分都是非线性函数,因此,底层优化问题是一个带约束的非线性规划问题。上层优化实现微电网运营商利益最大化的目标。当存在多个竞争主体时,市场达到均衡的条件是各主体都不主动改变自身的报价策略,即达到纳什均衡[21]。因此,上层优化问题实质上是一个博弈问题。以下针对双层问题的特点,分析相应的求解方法。
2.1 底层优化问题
底层问题的优化变量为DSO向各个微电网运营商和批发市场购买的功率,核心在于如何分配各售电方的中标功率,在满足系统安全运行约束的基础上,实现系统经济性最优的目标。对于此问题,本文采用跟踪中心轨迹内点法进行求解[22],其紧凑形式如下:

根据拉格朗日函数极小值存在的必要条件和相应的KKT条件,可得到一系列非线性方程组,最后利用牛顿-拉夫逊法对该方程组进行求解,即可得到DSO的最优经济调度方案。具体的求解流程在文献[22]中有详细描述,在此不再赘述。
底层优化问题求解实现后,DSO下发各微电网运营商的中标量和市场出清电价,微电网运营商根据市场的出清信息更新自身报价,直至市场达到纳什均衡。
2.2 上层博弈问题
上层问题的优化变量为微电网运营商m的报价,核心在于求取微电网运营商m针对其余运营商报价的最优报价策略。假定微电网运营商之间能够根据历史交易数据获知彼此的报价区间,且批发市场各时段的日前节点边际电价已知。由式(1)可知,目标函数是关于优化变量的隐函数,微电网运营商m的报价将影响中标的功率和市场的出清电价,从而影响其收益。
基于以上分析,本文采用遗传算法对该问题进行求解。种群的每个个体代表微电网运营商m的一种报价策略,通过对种群个体的自然选择,可以获得微电网运营商m的最优报价策略。
2.3 双层优化求解方法

基于以上分析,针对本文所提出的多微电网参与下的配电侧电力市场竞价模型求解流程见图3。
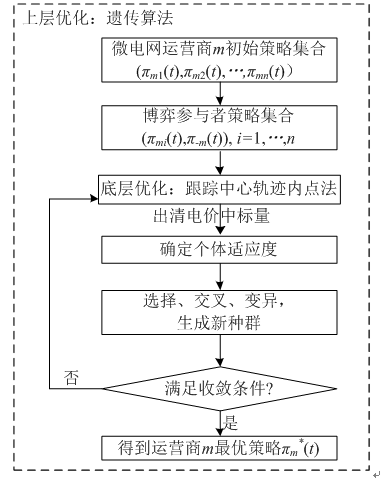
图2 双层优化算法结构
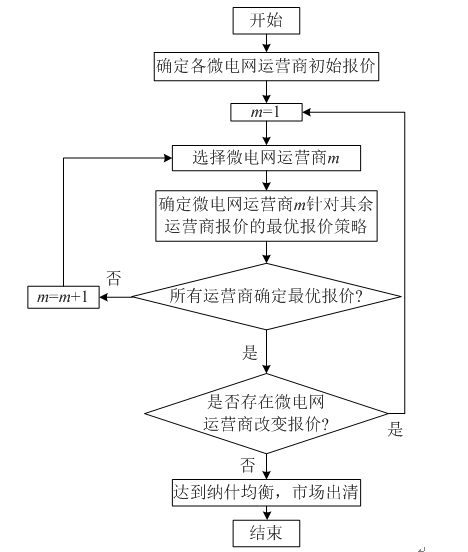
图3 广义纳什均衡求解流程
1)设置各微电网运营商的初始报价。
2)假定其余运营商报价固定,根据图2所示方法求解微电网运营商m的最优报价。
3)对所有微电网运营商重复步骤2),求出所有运营商的最优策略集合。
4)比较微电网运营商前后两次的报价是否发生改变,若存在任一运营商的报价改变,则返回步骤2),直至所有运营商都不再改变报价。
对于式(4)所示的微电网联盟的情况,优化变量为联盟体内各个微电网的最优报价,采用遗传算法求解时,每个个体包含Ne-Ns+1个变量,对应联盟体内各个微电网的一种报价策略,个体适应度为联盟内微电网收益的总和。基于图2所示的原理,可以得到联盟体微电网针对其余微电网的最优报价,即联盟内的任何一个微电网改变报价都无法提高整体收益。
3 算例分析
为了验证本文所提出的双层优化方法的可行性,本文以IEEE 33节点系统为例,对配电侧日前电力市场交易进行仿真模拟。考虑配电市场中包含3个微电网,分别位于系统的12、24和30节点[23],系统结构如图4所示。
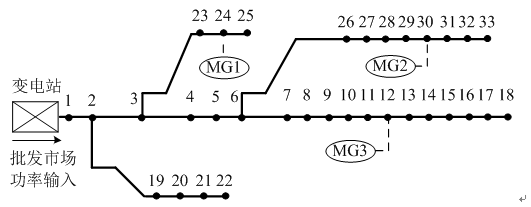
图4 IEEE 33节点配电系统结构
仿真中设定各售电方的初始报价等于批发市场的节点边际电价,仿真时段为第2日0—1 h。在该时段内的负荷需求为2.6+j1.6 MVA;批发市场节点边际电价为0.0762 USD/(kW•h);3个微电网的竞价功率范围设定为0~2 MW;DSO向批发市场购电的范围为0~3 MW;配电系统中各节点的电压上下限为0.95~1.05 pu。以下从微电网运行成本、微电网联盟以及微电网提供无功辅助服务3个方面对本文所提出的双层优化算法进行仿真分析。
3.1 不同运行成本下的竞价博弈仿真
在图1所示的电力市场中,微电网运营商的发电成本对其竞价策略和收益水平都有着显著的影响。因此,本文首先对不同运行成本下微电网运营商的竞价策略和市场的运行进行分析,仿真场景如表1所示。
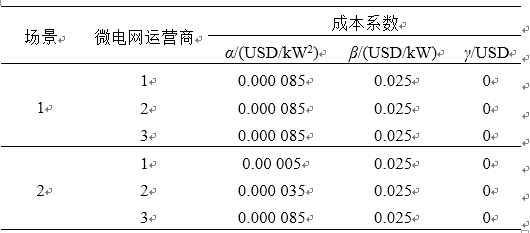
表1 运行场景设置
场景1和场景2的仿真结果分别如图5、图6和图7、图8所示。其中,图5、图7表示对应场景下各微电网运营商的竞价曲线;图6、图8表示对应场景下各售电方的净利润和有功功率中标量。
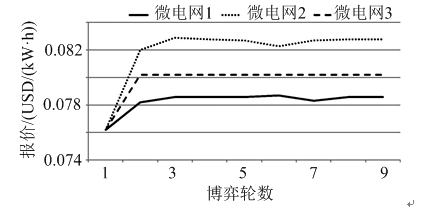
图5 场景1微电网运营商竞价曲线
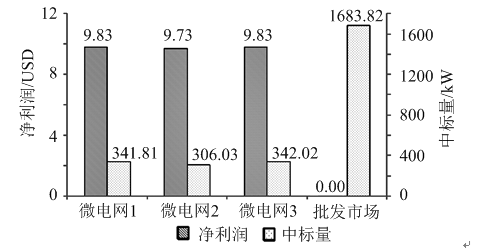
图6 场景1微电网运营商净利润及中标量
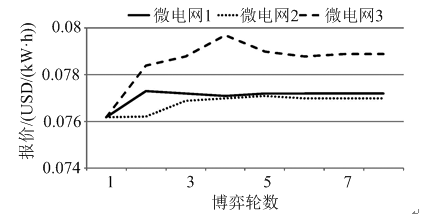
图7 场景2微电网运营商竞价曲线
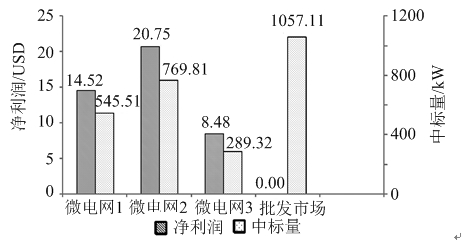
图8 场景2微电网运营商净利润及中标量

责任编辑:李鑫
免责声明:本文仅代表作者个人观点,与本站无关。其原创性以及文中陈述文字和内容未经本站证实,对本文以及其中全部或者部分内容、文字的真实性、完整性、及时性本站不作任何保证或承诺,请读者仅作参考,并请自行核实相关内容。
我要收藏
个赞