在竞争激烈的电力市场中 各售电主体如何优化交易策略使其收益最大？

摘要

随着市场改革逐步深入,大量社会资本涌入售电侧展开激烈竞争,未来电力市场交易必然存在多个虚拟电厂参与的格局,且各虚拟电厂内部风电等清洁能源存在不确定性,基于此,构建了多虚拟电厂非合作动态博弈日前市场优化交易模型。各主体充分考虑需求响应和电动汽车等为运行约束,采用市场模拟出清来表征其他虚拟电厂对自身决策的作用关系,并通过库恩-塔克(Karush-Kuhn-Tucker,KKT)条件等值表达,以收益最大化为目标制定最优竞标方案。此外,考虑虚拟电厂内部可再生能源出力不确定性以及控制对象的调节能力,将确定性竞标模型扩展为两阶段鲁棒优化模型,并通过列约束生成算法对主子问题进行交替求解,其中子问题中利用强对偶理论及Big-M法对max-min模型进行对偶并线性化处理。最后通过对整合不同分布式能源的多虚拟电厂系统进行算例分析,为虚拟电厂市场交易提供思路和参考。

关键词 : 多虚拟电厂;电力市场交易; 博弈论; 鲁棒优化;

（来源：电网技术 作者：周博, 吕林, 高红均, 刘俊勇, 陈庆攀, 谭心怡）

0 引言

随着《关于进一步深化电力体制改革的若干意见(中发[2015]9号》的发布,大量社会资本涌入电力市场展开激烈竞争[1],市场参与者分属不同的利益主体呈现多元化的趋势,各自整合不同的资源优化自身运行目标,在决策时需充分考虑各主体相互间的影响[2]。而虚拟电厂(virtual power plant,VPP)能有效整合分散的不同容量等级的分布式能源作为整体参与电力市场[3],具有更强的市场竞争力及稳定性,受到社会资本的青睐。因此研究虚拟电厂在竞争环境下的市场交易尤为必要。

目前关于虚拟电厂市场交易研究主要包括：文献[4]VPP整合储能及风电等分布式能源,构建改进多阶段随机规划模型优化VPP短期市场竞标策略。文献[5-6]以日前市场和平衡市场为背景,构建含间歇性电源、储能设施和可调度电厂的VPP购售电模型。文献[7]进一步研究了VPP同时参与多类市场下的竞标问题。上述文献对虚拟电厂市场交易奠定了重要的理论基础,但仍存在如下问题：一是未考虑虚拟电厂对市场出清结果的影响,仅作为价格接受者参与市场运行,本质上仍为VPP内部优化;二是市场环境单一,未充分考虑竞争对手决策行为对自身优化策略的影响,在多元化且竞争激烈的电力市场中无实际参考价值。在多VPP参与的市场中,各主体需综合其余竞争者的市场行为制定竞标策略,影响出清结果实现自身收益最大化,属于典型的多主体决策问题,博弈论能有效解决不同主体之间利益冲突问题[8-10]。文献[11]构建风火网3方非合作博弈模型,切实解决了各主体利益分配问题。文献[12]研究了日前调度、时前调度和实时调度相结合的多时间尺度滚动调度策略,基于需求响应和博弈论构建多VPP交互式调度模型。因此,可构建非合作博弈模型对多虚拟电厂市场交易行为进行优化。

同时,可再生能源出力的不确定性给VPP决策和安全运行带来极大的挑战,合理考虑不确定性因素的影响,制定经济可靠的交易策略,成为VPP市场交易问题研究的关键。鲁棒优化采用不确定集表征参数不确定性,克服随机规划中不确定参数概率分布难以准确获取的困难,且决策方案可以根据鲁棒系数灵活调节,实现经济可靠运行。文献[13-14]采用随机规划法处理不确定性,通过有限的场景模拟不确定参数,无法真实反映变量的实际情况,决策结果不能有效抵御潜在风险。文献[15]采用多面体不确定集表征风电、光伏的不确定性,构建清洁能源高渗透率下的鲁棒经济调度模型,提升调度方案的鲁棒性。文献[16]根据参数的调节能力,构建两阶段鲁棒优化模型,与传统鲁棒优化相比,两阶段鲁棒部分决策变量可随实际情况灵活调节,系统鲁棒性和经济性都得到极大提升。

基于上述分析,本文考虑市场参与者为价格制定者构建多主体非合作博弈模型,所有竞标主体计及其余竞争者的竞标影响分别寻求使得自身收益最大化的最优竞标策略,直至任何主体都不能从单方面改变竞标策略中获益,即达到纳什均衡。首先建立各虚拟电厂确定性优化竞标模型,并采用KKT条件及二进制扩充法将模型转化为混合整数线性规划模型。然后考虑风电等不确定性的影响,将确定性的线性模型扩展为两阶段鲁棒优化模型,并采用列约束生成算法(column and constraint generation,CCG)将模型分解为主问题和子问题,紧接着利用强对偶理论及Big-M法将子问题解耦并线性化,通过子问题与主问题交互迭代求解最优竞标策略。最后通过对整合不同分布式能源的多虚拟电厂系统进行算例分析,为虚拟电厂市场交易提供思路和参考。

1 非合作博弈框架

新一轮电力市场改革放开配售电市场,引入多方竞争,各利益主体分别整合不同分布式能源最大化运行目标,相互竞争却也相互依存。因此在深化改革的电力市场环境下,以虚拟电厂运营商个体或联盟作为博弈的参与者,决策方案必须充分考虑其他运营商的策略信息,VPP运营商i以最大化效益函数Gi为目标决策竞标策略si,从而建立多虚拟电厂非合作博弈市场交易模型：F=(S1,⋅⋅⋅,Sn;F=(S1,⋅⋅⋅,Sn;G1,⋅⋅⋅,Gn)G1,⋅⋅⋅,Gn)。模型中纳什均衡解为博弈的最优决策方案,任何主体都不能从单方面改变纳什均衡中获益。此时该博弈模型的纳什均衡最优解(s∗1,s∗2,⋅⋅⋅s∗n)(s1∗,s2∗,⋅⋅⋅sn∗)应满足Gi(s∗i,s∗−i)≥Gi(si,s∗−i) Gi(si∗,s−i∗)≥Gi(si,s−i∗) ∀i∈I ∀si∈Si∀i∈I ∀si∈Si,其中“-i”表示除虚拟电厂运营商i外的其余博弈参与者。

多虚拟电厂市场交易结构如图1所示,虚拟发电厂通过整合分散的不同容量等级的分布式能源,如可再生能源(风电、光伏)、燃气轮机、储能以及柔性负荷等,从而作为整体参与电力市场交易,合理预测内部资源信息及竞争者的报价数据,基于上述非合作博弈模型求解最优竞标策略,并上报给调度中心;调度中心在接收到各VPP运营商提交的竞标策略和负荷信息之后,在满足市场负荷需求的前提下,确定统一市场出清价及各VPP中标电量,最大化社会效益。

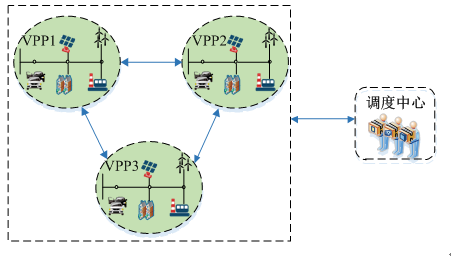
2 各VPP两阶段鲁棒竞标模型

2.1 各VPP确定性竞标模型

2.1.1 目标函数

VPP运营商i根据掌握的市场信息和其余虚拟电厂竞标历史数据模拟得到负荷需求量dˉdˉ及竞争

4 算例分析

4.1 算例参数

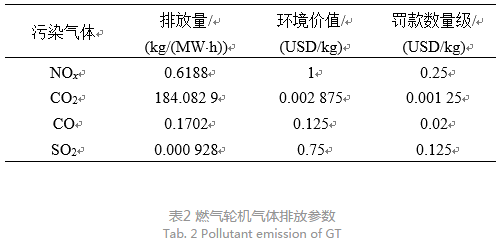
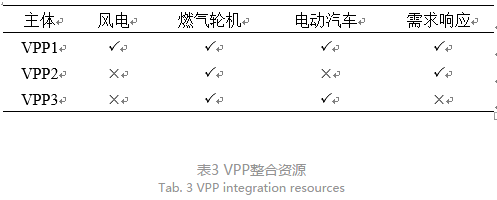
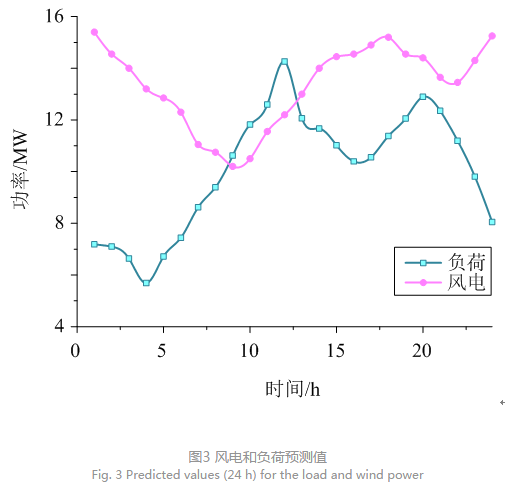
算例采用含3个虚拟电厂的系统构成博弈环境,各虚拟电厂参数及内部结构如表1—3所示,其中燃气轮机型号为TAU5670,GT参数和污染气体排放参数详见文献[7];PSDR基线负荷占总负荷的30%,电价折扣率及弹性系数等相关参数取自文献[18];各虚拟电厂24时段负荷数据和可再生能源出力预测值示于图3;电动汽车由24 kW·h家用型尼桑LEAF[21]组成,文献[23]指出电动汽车出行和

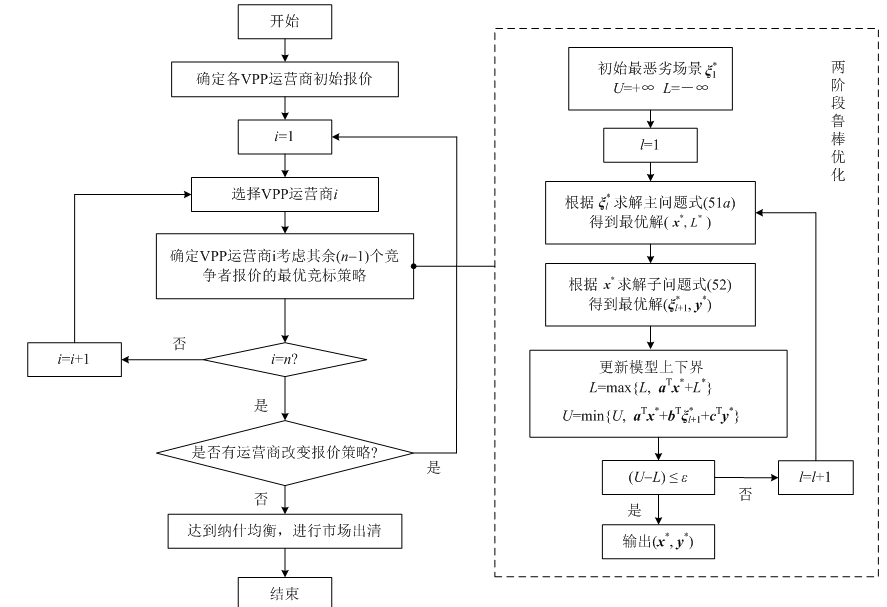
图2 纳什均衡求解流程图

表1 燃气轮机参数

Tab. 1 Parameters of GT

返回时刻服从正态分布,行驶距离服从对数正态分布,对应的概率密度函数为f(ts), f(te), f(dv),本文采用蒙特卡罗方法对每辆电动汽车的行驶距离和并网时间进行模拟,生成图4—5所示的1000辆电动汽车单一时刻驶入和驶离的电动汽车数量及行驶距离输入数据,最后采用K-means聚类算法抽取10类典型电动汽车进行优化,降低计算维度。选取出

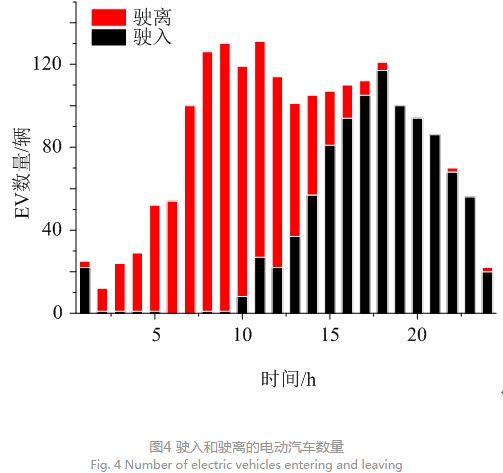
行、返回时刻及行驶距离的均值和方差分别为(17.47, 3.41),(8.92, 3.24),(4, 0.8)。

4.2 结果分析

各VPP根据表3所示的内部组成元素,分别选择对应成本函数及约束条件构成目标函数,构成含3个虚拟电厂的非合作博弈模型,根据图2所示流程对非合作博弈模型进行求解。经过25轮博弈之后各VPP收益趋于稳定,VPP1-3均不能从单方面改变自身策略来获取更多收益,此时的竞标策略即为使得各主体收益最优的纳什均衡解,VPP1-3对应的均衡收益(USD)分别为7232.51、2615.04、3182.24。

4.2.1 多虚拟电厂博弈结果

基于上文所述的算例系统,调度中心收到各VPP运营商提交的竞标策略和负荷信息之后,在满足市场负荷需求的前提下,确定统一市场出清价及各VPP中标电量,最大化社会效益。各虚拟电厂非合作博弈环境下的出清结果如图6所示。

从图中很明显可以看出VPP1的中标量最大,也就是VPP1在博弈中占据绝对优势,而VPP2中标量较少,甚至出现竞标失败的情况,结合VPP的内部构成以及相关参数可以证实此结论。VPP1整

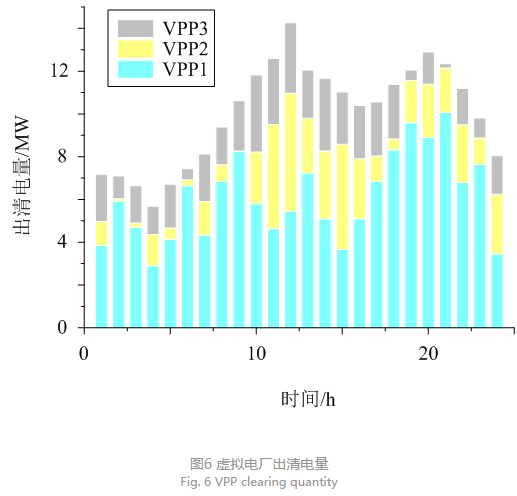
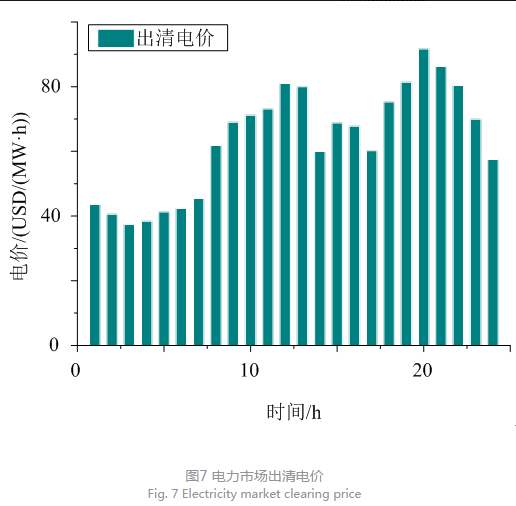
合风电作为可再生能源,且聚合电动汽车及电价型柔性负荷来平抑风电出力的波动。风电作为清洁能源虽然出力随机性大,但其较低的运行成本使得VPP1在博弈竞标中处于较低报价水平,且电动汽车及电价型柔性负荷为其稳定运行提供双重保护;相反VPP2及VPP3的竞标主要取决于燃气轮机的出力,较高的运行成本使得虚拟电厂只能提高报价以最大化竞标收益,这也使其在非合作博弈中处于劣势;VPP3对内部大量处于停驶状态的电动汽车进行有序管理,优化其充放电时间,使其在竞标中具有较高的竞争力,因此出清电量高于VPP2。VPP1的运行模式可为实际运营商提供参考,使其在现实竞标环境中获得较大成功。相应的竞标电价见表4,单位为USD/(MW•h)。电力市场出清电价见图7。

4.2.2 VPP1的调度情况

归根结底,VPP整体竞标能力受内部各元件出力的影响,从功率平衡约束可看出,内部元件的调度计划直接决定VPP的出力值大小;且内部元件成本函数各异,优化调度组合计划能在保证VPP整体出力的前提下降低运行成本,提升其在非合作博弈中的话语权,以低电价-高电量在竞标中获得成

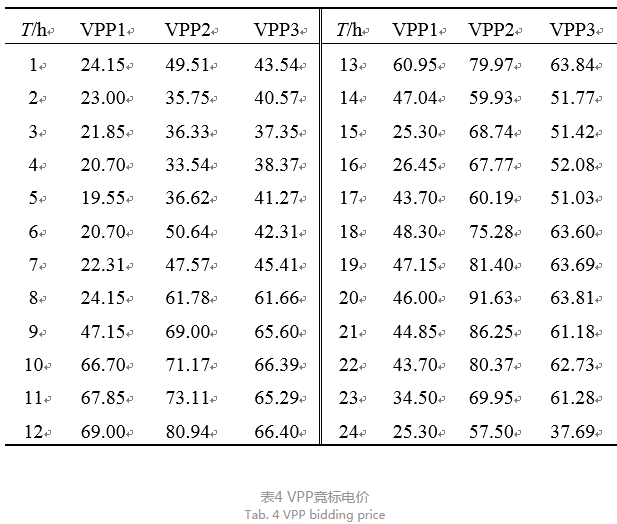
表4 VPP竞标电价

Tab. 4 VPP bidding price

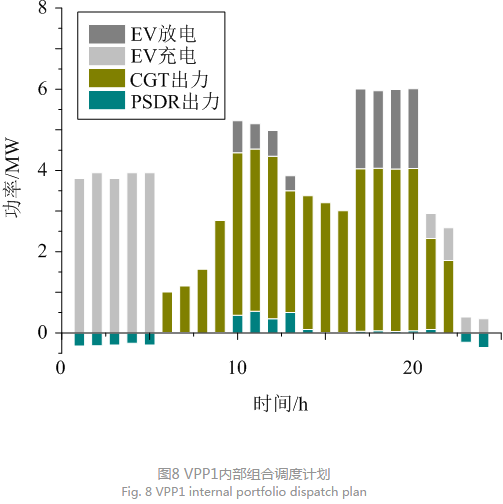
功。此处以VPP1为例分析其最优调度组合,各元件出力情况如图8所示,其中PSDR出力为负时表示增加负荷,为正时表示降低负荷。

由于不可控可再生能源的波动,VPP1中可控资源的出力相应地改变。在夜间(0—5 h)风电出力较大,PSDR受低电价及优惠折扣R的激励增加耗电量(如工厂在夜间开机);结合图4—5呈现的EV行驶规律,90%电动汽车在该时段处于停驶状态,所以电动汽车大多选择在该时段充电以储备行驶所需的电量;不仅如此在第1个高峰负荷时段,电动汽车联网放电缓解VPP出力不足,在第2个高峰负荷时段电动汽车因其电池储能有限,需调用PSDR削减负荷,为VPP提供虚拟出力。可以看出电动汽车作为移动负荷,同时也具有储能的特性,结合电动汽车行驶规律优化其充放电行为再辅以PSDR能为VPP提供双重保护,平抑可再生能源出力波动。从整体收益及成本值可以看出这样的组合调度模式能降低VPP运行成本,提升其竞标收益。

4.2.3 两阶段鲁棒优化和静态鲁棒方法对比分析

1)CCG算法有效性分析。

活调整交易策略的鲁棒性。CCG算法迭代次数和计算时间如表5所示,收敛精度ε为0.001。可以看出两阶段鲁棒优化模型的迭代次数较少,这表明CCG算法能够快速识别出最恶劣场景,对两阶段鲁棒优化模型进行有效求解;随着βW的增加,计算时间成本和迭代次数均有不同程度的增大。

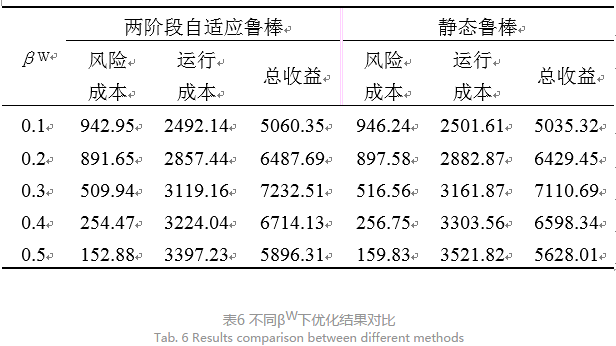
2)为有效分析本文所提两阶段鲁棒优化方法应对不确定性的能力,VPP1分别采用静态鲁棒、两阶段鲁棒优化模型优化交易策略,各模型运行结果如表6所示。

从表6横纵向对比可以看出：1)随着不确定集的增大,风险成本呈下降趋势,运行成本呈上升趋势,总收益先增加后减小,在0.3处取得最大。结合2.2节可以看出,随着不确定集增加,风电出力波动区间越大,意味着交易策略能够应对更为极端的风电恶劣场景,因此能有效降低风电波动导致的弃风及切负荷量,进而风险成本随之减少;对运行成本而言,VPP需要加大可控燃气轮机组出力,以保证有足够应对风电波动的动态备用容量,这就导致运行成本增加,系统经济性下降。2)与两阶段鲁棒相比,静态鲁棒的运行成本、风险成本增大,总收益减小。这是因为两阶段鲁棒模型将部分决策变量(如：燃气轮机、可中断负荷等出力)放在内层优化中,能够针对不确定参数情况进行适应性调节,无需提前确定。因此相比静态鲁棒优化,两阶段鲁棒优化交易方案具有更强的抵御风险能力,经济性和鲁棒性得到极大的改善。

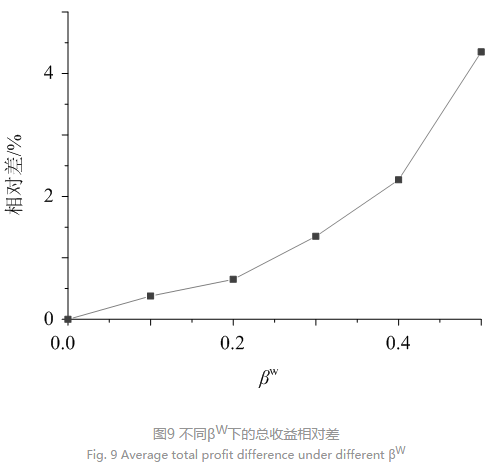
为了更清晰的对比两阶段鲁棒优化和静态鲁棒方法的性能,定义如下总收益相对差指标ΔG：

显然,相比静态鲁棒方法,两阶段鲁棒优化具有更好的经济性。随着βW的增大,两阶段鲁棒与静态鲁棒总收益相对差增大,表明两阶段鲁棒优化交易策略更能抵抗系统的不确定性。

5 结论

本文采用多虚拟电厂建立非合作博弈模型,各主体充分考虑其余竞争者的策略影响分别追求利益最大化。通过对整合不同分布式能源的多虚拟电厂系统进行算例分析得到以下结论：1)虚拟电厂整合资源对出清结果有着较大影响,较低的运行成本能够使得虚拟电厂处于低报价水平,在竞标中获得较大成功;2)聚合电动汽车并优化其充放电行为能够稳定虚拟电厂整体出力,提升其在电力市场中的竞争力;3)采用切负荷和弃风成本量化不确定性带来的风险,决策方案需兼顾鲁棒性与经济性,单方面的考虑鲁棒性或经济性都会导致虚拟电厂收益下降。

本文主要围绕电量交互形式进行优化,下一步将对VPP要素进行丰富,跳出以电为中心的思路,重点研究蓄冷蓄热等综合能源服务下的交易策略。

参考文献

[1] 中国中央国务院.关于进一步深化电力体制改革的若干意见[EB/OL].(2015-03-31)[2017-08-31]..

[2] 艾欣,周树鹏,赵阅群.含虚拟发电厂的电力系统优化运行与竞价策略研究[J].中国电机工程学报,2016,36(23):6351-6362. Ai Xin,Zhou Shupeng,Zhao Yuequn.Optimal operation and bidding strategies of power system with virtual power plants[J].Proceedings of the CSEE,2016,36(23):6351-6362(in Chinese).

[3] 陈春武,李娜,钟朋园,等.虚拟电厂发展的国际经验及启示[J].电网技术,2013,37(8):2258-2263. Chen Chunwu,Li Na,Zhong Pengyuan,et al.Review of virtual power plant technology abroad and enlightenment to China[J].Power System Technology,2013,37(8):2258-2263(in Chinese).

[4] 马春艳,董春发,吕志鹏,等.计及随机因素的商业型虚拟发电厂短期交易与优化运行策略[J].电网技术,2016,40(5):1543-1549. Ma Chunyan,Dong Chunfa,Lü Zhipeng,et al.Short-term trading and optimal operation strategy for commercial virtual power plant considering uncertainties[J].Power System Technology,2016,40(5):1543-1549 (in Chinese).

[5] Kardakos E G,Simoglou C K,Bakirtzis A G.Optimal offering strategy of a virtual power plant:a stochastic bi-level approach[J].IEEE Transactions on Smart Grid,2016,7(2):794-806.

[6] Pandžić H,Morales J M,Conejo A J,et al.Offering model for a virtual power plant based on stochastic programming[J].Applied Energy,2013,105(5):282-292.

[7] 周亦洲,孙国强,黄文进,等.计及电动汽车和需求响应的多类电力市场下虚拟电厂竞标模型[J].电网技术,2017,41(6):1759-1766. ZHou Yizhou,Sun Guoqiang,Huang Wenjin,et al.Strategic bidding model for virtual power plant in different electricity markets considering electric vehicles and demand response[J].Power System Technology,2017,41(6):1759-1766(in Chinese).

[8] Heifetz A.Game theory:interactive strategies in economics and management[M].Cambridge:Cambridge Univ.Press,2012:1-2.

[9] Myerson R B.Game theory:analysis of conflict[M].Harvard University Press,1997.

[10] 赵敏,沈沉,刘锋,等.基于博弈论的多微电网系统交易模式研究[J].中国电机工程学报,2015,35(4):848-857. Zhao Min,Shen Shen,Liu Feng,et al.Research on trading patterns of multi-microgrid systems based on game theory[J].Proceedings of the CSEE,2015,35(4):848-857(in Chinese).

[11] 赵文会,闫豪楠,何威.基于风火网非合作博弈的电力市场均衡模型[J].电网技术,2018,42(1):103-109. Zhao Wenhui,Yan Haonan,He Wei.Power market equilibrium model based on wind-fire network non-cooperative game[J].Power System Technology,2018,42(1):103-109(in Chinese).

[12] Wang Y,Ai X,Tan Z,et al.Interactive dispatch modes and bidding strategy of multiple virtual power plants based on demand response and game theory[J].IEEE Transactions on Smart Grid,2016,7(1):510-519.

[13] Tajeddini M A,Rahimi-Kian A,Soroudi A.Risk averse optimal operation of a virtual power plant using two stage stochastic programming[J].Energy,2014,73(9):958-967.

[14] Shayegan-Rad A,Badri A,Zanganeh A.Day-ahead scheduling of virtual power plant in joint energy and regulation reserve markets under uncertainties[J].Energy,2017,121.

[15] 梁子鹏,陈皓勇,王勇超,等.含电动汽车的微网鲁棒经济调度[J].电网技术,2017,41(8):2647-2656. Liang Zipeng,Chen Haoyong,Wang Yongchao,et al.Robust economic dispatch of microgrids containing electric vehicles[J].Power System Technology,2017,41(8):2647-2656(in Chinese).

[16] 仉梦林,胡志坚,李燕,等.基于可行性检测的考虑风电和需求响应的机组组合鲁棒优化方法[J/OL].中国电机工程学报,DOI:10.13334/j.0258-8013.pcsee.170654. Yu Menglin,Hu Zhijian,Li Yan,et al.A robust optimization method for unit combination considering wind power and demand response based on feasibility detection[J/OL].Proceedings of the CSEE,DOI:10.13334/j.0258-8013.pcsee.170654(in Chinese).

[17] 左坤雨,刘友波,向月,等.基于信息互动的分布式可再生能源多代理交易竞价模型[J].电网技术,2017,41(8):2477-2484. Zuo Kunyu,Liu Youbo,Xiang Yue,et al.Multi-agent transaction bidding model for distributed renewable energy based on information interaction[J].Power System Technology,2017,41(8):2477-2484(in Chinese).

[18] 牛文娟,李扬,王蓓蓓.考虑不确定性的需求响应虚拟电厂建模[J].中国电机工程学报,2014,34(22):3630-3637. Niu Wenjuan,Li Yang,Wang Beibei.Demand response based virtual power plant modeling considering uncertainty[J].Proceedings of the CSEE,2014,34(22):3630-3637(in Chinese).

[19] 赵兴勇,王帅,吴新华,等.含分布式电源和电动汽车的微电网协调控制策略[J].电网技术,2016,40(12):3732-3740. Zhao Xingyong,Wang Shuai,Wu Xinhua,et al.Coordinated control strategy research of micro-grid including distributed generations and electric vehicles[J].Power System Technology,2016,40(12):3732-3740(in Chinese).

[20] Bakirtzis A G,Ziogos N P,Tellidou A C,et al.Electricity producer offering strategies in day-ahead energy market with step-wise offers[J].IEEE Transactions on Power Systems,2007,22(4):1804-1818.

[21] Fotouhi A,Auger D J,Propp K,et al.A review on electric vehicle battery modelling:from Lithium-ion toward Lithium-Sulphur[J].Renewable & Sustainable Energy Reviews,2016(56):1008-1021.

[22] Zeng B,Zhao L.Solving two-stage robust optimization problems using a column-and-constraint generation method[J].Operations Research Letters,2013,41(5):457-461.

[23] 许少伦,严正,冯冬涵,等.基于多智能体的电动汽车充电协同控制策略[J].电力自动化设备,2014,34(11):7-13. Xu Shaolun,Yan Zheng,Feng Donghan,et al.Collaborative ging strategy for electric vehicles based on multi-agent[J].Electric Power Automation Equipment,2014,34(11):7-13(in Chinese).