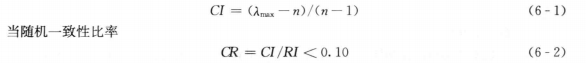电力企业无功优化控制分析论文

摘要: 提出了一种基于混沌算法的主动禁忌混合混沌算法(RTSCOA),该算法结合了混沌算法的全局遍历性和禁忌算法的“记忆”功能,利用主动禁忌法的反馈机制控制管理禁忌表长度,能够有效地跳出局部极小点。分别对IEEE6和IEEE30节点进行仿真,并与标准遗传算法/改进遗传算法(SGA/AGA)进行比较,以证明该算法在电力系统无功控制中应用的有效性。经比较,该方法较其他算法在计算速度、寻优能力上有一定的提高。

电力系统无功优化是最优潮流[1]的一部分,通过无功调节设备改变系统的无功潮流分布,减少系统有功网损,实现电网的经济运行。传统无功优化求解方法有线性规划法、非线性规划法和动态规划法等[2],利用传统方法精确求解无功优化问题比较困难。基于混合混沌优化算法利用混沌系统的一些独特动力学性质直接采用混沌变量进行解空间的遍历搜索,搜索过程按混沌运动自身规律进行,与一般启发式搜索算法相比它不需要启发信息,因此更易于跳出局部最优解,适合全局优化搜索,并且不要求优化模型具有连续性和可微性。混沌优化方法已用于机械、化工、管理和电力等领域[3～6]。

1无功优化模型的数学描述

电力系统无功优化问题是一个多变量、非线性、多约束的组合规划问题,其控制变量既有连续变量(节点电压),又有离散变量(有载变压器分接头、补偿电容器/电抗器投切组),连续变量和离散变量之间又不相互独立,使得优化过程十分复杂。选择发电机节点电压幅值、无功补偿源节点的注入无功及变压器的可调变压器分接头作为控制变量,同时考虑各种约束条件,建立无功优化数学模型。目标函数:F=minPL+i=1!λiTi"#(1)式中:PL为系统网损;i=1!λiTi为惩罚项;λi为惩罚因子。约束条件包括等式约束和不等式约束。等式约束:Pi=Vij∈i!Vj(Gijcosθij+Bijsinθij)Qi=Vij∈i!Vj(Gijsinθij-Bijcosθij%’’&’’()(2)不等式约束:U≤U≤UX≤X≤X%’&’((3)式(2,3)中:Pi和Qi分别为节点有功和无功功率;U=[VGi,QCi,KTi]为控制变量,U和U表示其上下限;X=[VLi,SLi,QGi]为状态变量,X和X表示其上下限;VGi为发电机端电压;VLi为节点电压;KTi为有载变压器分接头档位;QCi为补偿电容器投切容量;QGi为发电机无功出力;SLi为支路通过功率。

2主动禁忌混合混沌算法(RTSCOA)

2.1RTSCOA的原理文献[7]中F.Glover提出了禁忌搜索算法,利用历史纪录来指导下一步搜索方向,当到达局部最优解时将搜索方向指向导致目标函数退化最小的方向上,由此避开局部最优解。同时,通过将已执行过的移动设置为临时禁止来避免搜索重复的空间。传统禁忌搜索算法需要通过设置或者调整搜索参数来进行有效的搜索。主动禁忌算法[8]是主动搜索[9]算法中的一种,它通过反馈机制调节禁忌表长度,自动平衡集中强化搜索策略和分散多样化搜索策略。在算法进行搜索的过程中,所有被访问过的解都被储存起来,当执行一步移动时都要检查当前解是否已经访问过。如果一个解重复出现,禁忌表长度增大,变为原来的NI倍,NI为长度增加调节系数(NI≥1);反之,如果经相当长的时间后没有重复的解出现,禁忌表长度减小为NO,NO为长度减小调节系数(1>NO>0)。当某一个解的重复出现次数达到一定数量时,则通过在当前解的基础上移动几步来跳出,执行移动的步长在一定范围内随机产生。同时,为防止很快跳回已经搜索过的区域,所有随机操作均被禁止,这一机制可以使搜索有效地跳出局部极小点。

2.2RTSCOA的步骤

(1)初始化。k=0,选取n个随机混沌值y(k)i,并存储在禁忌表中。

(2)利用载波x(k)i=xi+y(k)i(xi-xi)将n个混沌随机变量映射到控制变量域内X。

(3)计算f(X),找到最小的f(X*),并且设f(X)current=minf(X*)以及对应的X*,fbest=f(X)current。

(4)如果变量为连续变量,利用xi=xi+εv对下次混沌映射初值进行更新。其中,ε取很小的数(ε=0.0001);v为(-1,1)之间的随机数。如果为离散变量,则在附近增加或减少一个步长,判断xi是否在禁忌表中。若在,则重选;若不在,则放到禁忌表中。

(5)增加迭代数y(k)i=4y(k-1)i[1-y(k-1)i],x(k)i=xi+y(k)i(xi-xi)。

(6)计算禁忌表中变量的f(X),比较fbest和f(X)current。如果fbest≤f(X)current,则fbest=f(X)current,否则不替换。

(7)k=k+1,判断总次数以及fbest是否多次不变,否则返回(3)。

(8)输出结果。

3无功优化的混合混沌算法实现

利用RTSCOA求解电力系统无功优化问题时,由于混沌算法的遍历性经过一定的求解过程可以将变量带到最优解附近,此时并不要求获得精确解,利用主动禁忌算法的“记忆”功能将变量在最优解附近增加一微小量,并将搜到的解存储在禁忌表中。在搜索过程中,算法将搜索到的当前解不断地存储到禁忌表中,同时不断地释放已经到期禁忌表的解,求解的过程中需注意以下问题。

(1)无功优化模型的确定无功优化模型的数学表达式如下:F=min"PL+λ1Ni=1#(Vi-VilimVimax-Vimin)2+λ2Mj=1$(QGi-QGlimQGimax-QGimin)2+λ3Lk=1$(SLi-SLilimSLimax-SLimin)2%(6)当Vi≥Vimax时,Vilim=Vimax;当Vi≤Vimin时,Vilim=Vimin,否则Vilim=Vi,发电机无功和支路功率作类似处理。λ1、λ2和λ3为惩罚因子,惩罚项包括电压越限、发电机无功和支路功率等惩罚项。

(2)优化变量的选择对于以有功网损最小为目标函数、考虑功率平衡约束和变量约束的无功优化问题,解向量包括控制变量U=[VGi,QCi,KTi]和状态变量X=[Vi,SLi,QGi],以控制变量为优化变量;对于发电机机端电压等连续变量直接利用“载波”映射将混沌变量变换到控制变量的限值区间;对于并联补偿电容器组和变压器变比等离散变量进行就近归整处理,增加或者减少一个步长来和禁忌表中的变量进行比较。

(3)禁忌表当前最优解邻域的移动根据变压器分接头及可投切电容器的动作特点,在次优解附近每次对一个变量执行加一操作,若超过变量定义范围,则该变量操作保持原值不变;对于发电机端电压等连续变量应增加一个微小量,选择邻域中不在禁忌表中的最优解作为找到的解,如果邻域中的解都被禁忌,则执行操作,选择目前为止最好的解作为当前解。超级秘书网

4仿真分析

本文利用IEEE30节点的仿真结果来验证本算法的有效性,利用Matlab6.5编程在P41.7GPC机上仿真运行。IEEE30系统中有41条支路、6个发电机节点和22个负荷节点,6个发电机节点为1、2、5、8、11、13;可调变压器支路为L6～9、L6～10、L4～12、L27～28;并联电容器节点为3、10、24,如图1所示。系统总的负荷Pload=2.834,Qload=1.262。假设发电机机端电压和变压器的变比均为1.0,通过潮流计算得到∑PG=2.893859,∑QG=0.980199,Ploss=0.059879。越限节点电压分别为:V26=0.932,V29=0.940,V30=0.928(数据均为标幺值);存在一个无功发电功率越限。通过仿真得到数据与其他无功优化算法进行比较。

5结论

混合混沌优化算法充分利用混沌算法和禁忌算法的各自的特点,在混沌搜索过程中利用禁忌算法禁忌表记忆能力将初解保存于禁忌表中。利用禁忌搜索算法将存放于禁忌表中的解增加一个微小量,进行比较存放于禁忌表,同时利用反馈机制对禁忌表长度进行控制。混合混沌优化算法在全局和局部都可以进行搜索,因而算法不会陷入局部最优解,并且具有较高的搜索效率,仿真结果显示混合混沌优化算法在电力系统无功电压控制应用的有效性。

参考文献:

[1]MAJT,LAILL,YANGYH.ApplicationofGeneticAlgorith-msinReactivePowerOptimization[J].ProceedingsoftheCS-EE,1998,15(5):347-353.

[2]张勇军,任震,李邦峰.电力系统无功优化调度研究综述[J].电网技术,2005,29(2):50-55.

[3]王洪章,熊信艮,吴耀武.基于改进Tabu搜索算法的电力系统无功优化[J].电网技术,2002,26(1):15-18.