CT系统参数标定问题的分析研究
CT系统参数标定问题的分析研究
严亚楠1,岳靓2,张子豪。
(1、华北水利水电大学数学与统计学院,河南郑州450046
2、华北水利水电大学管理与经济学院,河南郑州450046
3、中山大学数据科学与计算机学院,广东广州511400)
摘要:本文针对CT系统参数标定问题,通过绘制标定模板射线吸收强度变化图像,发现第278至168条射线在第151个方向时,与大椭圆切于短轴两端,相差110个探测器,对应大椭圆的短轴长30mm,从而标定探测器单元之间的距离。根据CT系统旋转的特性,可以确定旋转中心位于第256条射线到257条射线中间。根据第151和第61个方向时四条特殊射线的交点,确定旋转中心为(-9_0919, 6.6178)。,第223条射线在第151个方向时x射线衰减程度最高,即通过大椭圆长轴。,以大椭圆中心为原点,建立笛卡尔直角坐标系,即可标定初始位置与X轴成29度。
关键词:CT系统;参数标定;笛卡尔坐标
CT系统可以在不破坏样品的前提下,探测出样品的内部结构信息,因此在医学与工业上有着广泛的应用。X射线照射并穿过物体,接收器接收到的信号强度会因为穿过物体的厚度不同而接收到不同的数值。但在安装CT系统时,成像效果受多种因素影响,为了提高成像的精准度和稳定性,需要对CT系统的参数进行标定。
一、探测器单元间距离的确定
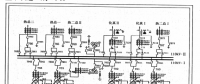
在MATLAB中绘制两个均匀固体介质组成的标定模板在180个方向上对X射线的吸收变化情况,如图所示。
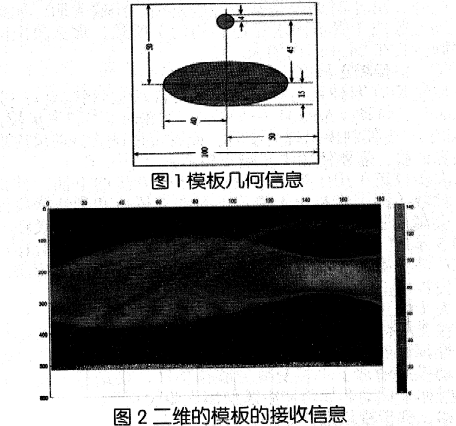
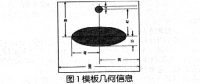
在正方形托盘上放置两个均匀固体介质组成的标定模板,模板的几何信息如图1所示。每一点的吸收强度相同,模板是均匀介质。假设探测器单元均匀分布,各探测器间距离相等,在第151次扫描结果中,第223个接收器,接收到了最弱的X射线信号,即衰减最强的信号。在第151次扫描结果中,此时的第223个接收器的射线与椭圆长轴重合,该时刻第278个到第168个与第74个到第46个接收器之间有效的接收到了信号,其中第278个到第168个接收器接收到的信号对应大椭圆的短轴,短轴长度30mm,第74个到第46个接收器接收到的信号对应小圆的半径,半径长度为8mm。由此可以推算出接收器的距离为0.2714mm(两组数据平均值)。
二、旋转中心位置的确定
CT系统围绕其中心旋转,X射线的发射器和探测器相对位置固定不变,该系统共有512组探测器,则旋转中心所枉轴线一定处于第256-2/57个探测器之间。
该探测器的射线在第61次照射时,发射器所发射的射线与大椭圆短轴平行,其中第379个探测器所接受射线与大椭圆相切与大椭圆长轴垂直,它与第256个探测器之间相隔123个等距即33.3822mm。
由于短轴半径为40mm,固第256条射线到大椭圆短轴的距离为6.6178mm。在第15 1次照射时,第223个接收器的射线与椭圆长轴重合,又由于旋转中心所在轴线一定处于第256-257个探测器之间,则旋转中心所在直线与大椭圆长轴之间间隔33.5个等距长度即为9.0919mm。
以大椭圆圆心为原点,以长轴为Y轴,以短轴为X轴,建立笛卡尔直角坐标系,则旋转中心的坐标为(-9.0919,6.6178)。
三、X射线180个方向的确定
(1)系统使用的X射线需要照射180个方向,由于X射线的发射器和探测器相对位置固定不变,故只要求出最开始的照射角度,随后每一次照射的角度均会随之确定。又由于在第151次照射时,X射线与X轴平行,敝初始照射角度与X轴成29度。该结果与照射模拟结果,第1()0,200,300,400个接收器位置处的吸收信息变化相符合,结果即图3所示。

四、结论
在本文CT系统中,射线通过椭圆的长轴时对应的衰减程度最大,由数据可知第223条射线穿过长轴的既不是转过150次时,也不是转过151次时,而是两次转动之间的某个时刻对应的某个角度。造成这种情况的原因有两点,一是原始数据本身存在误差,二是CT系统的旋转中心稳定性不强,导致在扫描的过程中照射角度产牛了偏差。
参考文献:
[1]张俊,闰镔,李磊,闫培,陆利忠,张峰,魏星.采用高频能量的CT几何参数自标定方法[J].红外与激光工程,2013, 42( 09): 2540-2546.
[2]张俊,闫镔,李籍,陆利忠,张峰.锥束CT系统旋转平移轨迹几何参数标定方法[J].强激光与粒子束,2013,25 (10):2693—2698.
作者简介:
严亚楠,华北水利水电大学数学与统计学院;
岳靓,华北水利水电大学管理与经济学院;
张子豪,中山大学数据科学与计算机学院。

责任编辑:继电保护
-
《电力设备管理》杂志读者俱乐部会员招募
2018-10-16电力设备管理杂志 -
云南能源职业技术学院
2018-06-05云南能源职业技术学院 -
中国科学技术大学热科学和能源工程系