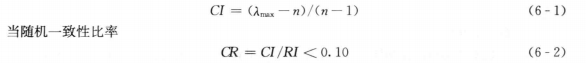磁悬浮列车动力学研究论文

针对车厢、悬浮转向架与轨道之间的耦合动力特性,武建军等通过对弹性变形轨道上2自由度磁悬浮列车耦合系统动力特性的数值研究,讨论了系统特征参数(悬浮体质量、运行速度、轨道长度等)对磁悬浮系统的动力学特性的影响方式,并分析了弹性轨道变形特性[29]。根据数值仿真结果,得出系统受控稳定性情况下的控制参数。谢云德等建立了轨道梁有限单元的动力学方程组,对轨道结构参数与频率、振型、极限速度之间的关系作了初步探讨,分析了车轨耦合系统发生自激振荡的原因,并对单铁加载试验过程中出现的自激振荡现象作出解释[30]。Y.Zhang等[31]根据机械悬浮车辆的实际参数,用随机振动理论对HTS型磁浮车进行了动力学分析,建立了简单的模型。这篇文献同样侧重数值仿真。S.Ohashi等[32]计算了有3个车厢、4个转向架的电磁式和电动式磁悬浮列车通过曲线时的位移和扭矩。

文献[33]中,XiaoJingZheng等将车辆的运动、轨道振动和控制系统相结合,针对5个自由度的二次悬挂体系的动力特性做了数值分析,并具体分析了在系统稳定时垂向和摇头运动的干扰范围和控制参数。分析表明,列车与轨道耦合系统的特性若忽略轨道变形,其结果是不同的。

4控制系统动力稳定性分析

磁悬浮列车的稳定性分为悬浮、导向和驱动3个方面。对电磁悬浮列车而言,由于电磁吸力与悬浮间隙的平方成反比关系,使得电磁悬浮系统本身存在固有的不稳定性。同时,磁悬浮列车的负载变化大,工作环境复杂,要求有控制能力强并对模型和参数变化不敏感的非线性控制系统与之相匹配。磁悬浮列车系统是多磁系统,它与单磁系统不同,当电磁铁提供最大升起力时,磁铁处在“力-距离特性曲线”中非线性部分。控制系统的增益与特性曲线上工作点的斜率成正比。因此,工作条件的变化将大大降低系统的瞬时特性,甚至会破坏稳定性。多磁系统还存在机车底盘上的磁铁多种机械解耦和各磁铁控制系统的机械解耦。因此,电磁型磁悬浮列车的稳定控制是很困难的。

在文献[20～22,26]中,动力控制系统往往被简化成等效弹簧,忽略了轨道变形对实际控制系统动力稳定性的影响。Meisenholder和Wang[34]曾用Laplace变换方法研究了刚性轨道的磁浮体铅直运动的稳定性[35]。周又和等[36]研究了悬挂式电磁悬浮体在铅垂方向运动的动力控制稳定性问题,对刚性轨道上的磁浮控制问题给出了控制参数的稳定区域。对于考虑了轨道弹性的磁悬浮动力系统,在对弹性轨道采用了振动模态函数展开后,其动力系统可由周期变系数的线性常微分方程组所描述。目前,对周期变系数线性常微分方程的动力稳定性分析多数是建立在Floquet理论基础上的[37～39]。陈予恕等指出在动力系统中,Lia2punov特性指数作为相邻轨线间的平均指数发散或收敛的指标,在研究系统混沌运动方面有重要作用[40]。

KruzerE发现,Liapunov特征指数等于其系数矩阵特征值的实部,当常系数线性常微分方程动力系统的所有Liapunov指数小于零时,动力系统是稳定的,否则,动力系统是不稳定的[41]。这一方法,避免了求解全部特征值后才能判别动力系统稳定性的不便。但对于由周期变系数线性常微分方程组描述的动力系统,没有给出用Liapunov特性指数判别系统稳定性的依据。周又和等针对这个问题,建立了特性指数与由理论得到的变换矩阵特征值之间的对应关系,并给出了用特性指数判别磁浮列车控制系统稳定性的方法[42]。

5结论

在磁场与承载能力的研究方面,在诸多文献中,单铁力的计算多是简化方法,忽略了漏磁通、磁心和导轨中的磁阻。然而,磁悬浮列车高速运行时产生的电磁阻力,将降低有效悬浮力,产生额外的磁势要求,并影响控制系统。电磁阻力的大小还直接影响到直线电机的驱动功率,对整个系统的运行经济性也有一定的影响[43]。建议:①在单铁力的计算中,考虑热损耗、漏磁通的影响,分析磁阻对有效悬浮力的影响;②在此基础上,建立在轨道平曲线和竖曲线处或轨道不平处,单铁力在垂直方向以外的力和力矩的计算公式和方法。

在磁悬浮列车动力学研究方面,主要集中于分析测试控制参数和系统特征参数对磁悬浮系统的动力特性影响。弹性轨道对动力控制稳定性及其动力特性有影响,这一点已为人们所接受。在研究磁力作用下轨道梁的特性基础上,建立了磁悬浮列车与弹性轨道耦合的铅垂方向的动力学模型。事实上,磁悬浮列车是一个复杂的多体系统,运动规律很复杂,除侧滚外(防侧滚梁限制),还有伸缩、侧移、升降及摇头、点头5个自由度,仅建立铅垂方向的模型不足以反映列车的运动状态。文献[33]中XiaoJingZheng等虽然针对5个自由度的二次悬挂体系的动力特性做了数值分析,但主要侧重于控制方面。

建议:①建立能反应每节车厢由4个完全相同但又独立控制的磁浮架的动力模型;②分别假设车厢为刚性和柔性,数值仿真模型列车通过平面曲线和竖曲线的情况;③分析悬浮列车启动时,列车与轨道共振的力学原理。

控制系统动力稳定性分析方面,主要根据系统动力特性的数值研究、数值仿真结果,得出系统受控稳定情况下的控制参数。在上述文献中,都没有考虑磁阻力的情况,也没有考虑诸如负载变化、强侧风、轨道附近有振(震)动源(诸如建筑工地打桩)、外界磁场波动等对磁浮系统的影响。在磁悬浮气隙不超过1cm,气隙波动控制在1mm的情况下,这些因素是否不予考虑,有待商讨。