光伏电站组件容量配比如何优化
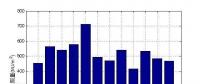
根据上图可得出如下结论:
(1)该地月总辐射量最大值发生在春、夏换季的5月;且全年逐月总辐射量较平均,有利于光伏电站平稳出力;
(2)该地年代表日总辐射极大值差异较小,4个年代表日差异主要是日照时长及当日天气情况而引起的日总辐射量的差异。
(3)该地5月至8月的正午(真太阳时)存在总辐射值超过1000W/m2的情况发生,根据对数据的分析。超过总辐射值超过1200W/m2在6月时有发生。
(4)该地10月至次年4月的空气质量好,透明度高,日总辐射值变化较平稳。
二、不同容量配置比值的计算
本文将采用基于实测的辐射数据完成光伏电站全年逐时(分钟)的发电功率计算。计算时根据如下步骤分别进行计算:
(1)光伏组件容量与逆变器容量配比值选择1、1.05、1.1、1.15、1.20分别计算全年逐时发电功率。
(2)考虑各光伏电站实际效率存在差异,光伏组件至逆变器直流母线的效率分别取80%、85%对步骤(1)的各计算结果进行折算。
(3)考虑到逆变器具备的短时超发能力,分别计算超过逆变器标称功率100%、105%、110%的能量损失。
(4)根据步骤(1)~(3)的计算结果,综合计算因光伏组件超配增发的功率与不同效率值、逆变器不同超发能力情况下而限电的最终增发的功率比值。
(5)光伏电站综合单位投资分别取7.5元/W(其中组件价格取3.5元/W)、8元/W(其中组件价格取4元/W)进行光伏电站新增投资比例的计算;
(6)综合步骤(4)、(5)的计算结论,计算△发电量与△投资的比值,其结果如下:
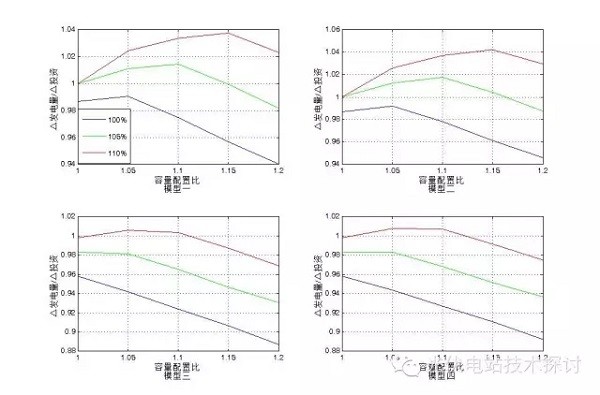
图4不同条件下△发电量/△投资分布曲线
因本文略去(1)~(5)的计算结果,对图4曲线说明如下:
(1)模型一:光伏组件至逆变器直流母线的效率取80%、投资8元/W(其中组件价格4元/W)的条件下分别计算步骤(1)中的各值,结果为步骤(3)中逆变器的各超发能力条件下的△发电量/△投资分布曲线;
(2)模型二:光伏组件至逆变器直流母线的效率取80%、投资7.5元/W(其中组件价格3.5元/W)的上述各条件下计算结果;
(3)模型三:光伏组件至逆变器直流母线的效率取85%、投资8元/W(其中组件价格4元/W)的上述各条件下计算结果;
(4)模型四:光伏组件至逆变器直流母线的效率取85%、投资7.5元/W(其中组件价格3.5元/W)的上述各条件下计算结果。
三、结论及建议
(1)建议光伏电站在前期设计中,应完成场址所在地的太阳能资源的实测工作,其将为电站的设备选型及后期分析提供必要的基础设计资料。本文分析结果仅适用于涉及场地的实测辐射数据,因各地的辐射数据、能量分布情况存在差异(见本文的(一)部分),如分析其他地区,需采用文章中方法进行重新计算、分析。
(2)不建议该地光伏电站的组件与逆变器容量配比取1:1。
从模型一~二结果得:无论逆变器是否具备超发能力,最优容量配比均大于1。当超过逆变器标称功率的100%、105%、110%时,其最优容量配比分别为1.05、1.1、1.15。
从模型三~四结果可以看出:当超过逆变器标称功率的100%、105%、110%时,其最优容量配比分别为1(即,此时再增加光伏组件容量,其收益将降低)、1~1.05、1.05~1.1。
(3)光伏电站实际效率的高低直接影响最优容量配比。随着电站效率的提高,最优配置比将减小。电站将因减少光伏组件的投入而降低初投资,同时还可提高电站收益。
(4)建议电站在设备选型时,应结合当地的太阳能资源合理选用具备短时超发能力的逆变器。
针对该地,其逆变器选型应要求其具备110%的短时超发能力(其超发时间的要求可根据计算的逐时发电功率进行统计分析)。在110%的超发能力下,模型一~二中的光伏电站采用的最优容量配置比取1.15,相应增加发电量为11.53%。
(5)该地光伏电站最优容量配置比不宜大于1.2。在模型一、二中:当最优容量配置比大于1.15时,发电量的增长将低于投资的增长;模型三、四中:当大于1.1时,亦出现上述情况。
(6)光伏电站最优容量配置比是的影响因素包括:太阳能资源、电站效率、逆变器超发能力、电站综合单价以及光伏组件单价等。
(7)由于电站效率为设计取值,投产运行的光伏因施工图设计的思路、设备选型、施工精度的管控、调试的消缺等原因,将引起电站的效率的差异。如可以预见电站的实际效率低于设计值,上述结论中的取值可适当加大;反之,应减小。
(8)本文的分析未考虑因光伏组件超配引起逆变器的实际工作效率的提高(本文的效率特指:光伏组件至逆变器的直流母线侧)。在电站实际运行后,实际运行数据将略高于本文中提高发电量的结论。
故光伏电站最优容量配置比应在设计前期结合上述各因素综合分析,以增强光伏电站的综合效益。

责任编辑:蒋桂云