深度丨考虑负荷发展和用户行为的分时电价优化研究
谭显东1,陈玉辰2,李扬2,井江波3,姜宁3,王子健2,沈运帷2
(1. 国网能源研究院有限公司,北京102209;2. 东南大学 电气工程学院,江苏 南京210096;3. 国网陕西省电力公司经济技术研究院,陕西 西安710075)
摘要:分时电价作为需求侧管理的一种重要经济手段,其在国内的全面实施势在必行,但电力需求的快速增长导致分时电价对用户的激励效果缺乏时效性。针对此问题,提出一种考虑负荷发展的分时电价优化方法,利用BP神经网络预测和灰色预测法预测出未来2年的典型日负荷曲线,将未来负荷曲线代入分时电价优化模型的结果作为电价约束,再对当年的典型日负荷曲线进行优化计算,得到合理的分时电价。算例将仅考虑当年典型日负荷曲线的优化结果与考虑负荷发展的优化结果进行对比,验证该优化方法延长分时电价时效的有效性。
0 引言
分时电价(time of use,TOU)是电力行业实施需求侧管理,鼓励用户改善用电方式,达到提高电力系统的负荷率和稳定运行目标的典型经济手段。随着电力体制改革加速,电力市场逐步推行,但中国仍处于电力市场化改革的过渡期,实时电价实施条件尚未成熟,分时电价方案的全面实施势在必行。分时电价把一天24h按负荷曲线划分成峰、平、谷3种时段,通过不同的时段电价引导用户多用低价谷电,少用高价峰电,以达到削峰填谷的目的 [1] 。由于各行业负荷曲线特性不同,各行业消费者对分时电价政策响应程度也有较大差异。合理的分时电价可以充分利用消费者心理,拉大峰谷电价差 [2] ,达到拉平负荷曲线的DSM目标。当前中国电力需求持续增长,负荷组成情况变化频繁,导致制定好的分时电价在一段时间之后对用户的激励效果变弱。因此,亟待解决上述问题。文献[3-4]提出了用户响应的概念,来描述电价对负荷的影响,并提出了基于需求侧管理的峰谷电价的数学模型,仿真出峰谷差价,为峰谷电价确定提供了一定的理论根据。文献[5]采用模糊聚类方法对峰谷时段进行重新划分,利用用户电力需求价格弹性矩阵,考虑尖峰电价的影响,激励用户改变用电行为。上述文献结合用户响应对分时电价作用机理进行分析,但均没有通过优化
模型制定电价,文献[6-7]结合消费心理学原理,设定了实施峰谷分时电价的目标函数,文献[8]采用非单纯形法对电价进行了优化,但均没有考虑随着负荷发展分时电价的激励效果减弱问题。本文针对分时电价对用户的激励效果时效性不足的问题,提出一种考虑负荷发展的分时电价优化方法,并通过算例将仅考虑当年典型日负荷曲线的优化结果与考虑负荷发展的优化结果进行对比,验证该优化方法的有效性。
1 典型日分时电价时段划分
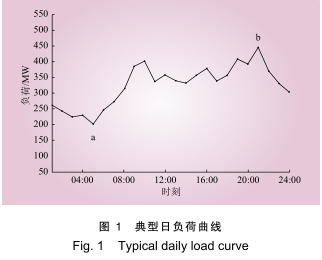
时段划分是分时电价制定的前提和发挥作用的重要保证[9-10]。不同用户由于其负荷特性存在较大差异,导致时段的划分结果不同。本文采用基于模糊数学的方法[11],以图 1 为例对分时电价时段划分方法进行阐述。
(1)确定典型日负荷曲线的最低负荷点 a 与最高负荷点 b,其中 a 点处于谷时段的可能性为100%,处于峰时段的可能性为 0,b 点处于峰时段的可能性为 100%,处于谷时段的可能性为 0;
(2)根据偏小型隶属度函数和偏大型隶属函数分别计算其余各点处于谷时段和峰时段的可能性,若某点峰时段可能性远大于其谷时段可能性,则该点归属于峰时段,若某点谷时段可能性远大于其峰时段可能性,则该点归属于谷时段,其余点归属于平时段;
(3)结合每段单独时段的时长≥2 h,且峰时段、平时段、谷时段的总时长均≥6 h 的约束,即可获得典型日负荷曲线的时段划分结果。
2 基于用户行为的分时电价作用机理
2.1 用户行为划分根据用户的电力消费行为受电价的影响程度,可以将用户分为顽固型、积极型、从众型3 种,以下从大工业用户、一般工商业用户和居民用户 3 类进行阐述。
(1)顽固型。该类用户对电价的响应程度较低。代表用户包括:①大工业用户中的石油加工业、钢铁制造业等,此类用户的设备连续生产,负荷曲线波动较小,负荷率较高;②一般工商业用户中的住宿餐饮服务业等典型服务业,其可调节负荷(如空调照明负荷等)与客户舒适度相关;③居民用户中的部分家庭人均收入较高者,此类用户对用电舒适度的敏感度普遍高于对用电成本的敏感度。
(2)积极型。该类用户对电价敏感,响应程度高。代表用户包括:① 大工业用户中的水泥等非金属矿物制造业、通用及专用设备制造业等,此类用户生产班制较为灵活且用电成本占生产成本比例较大;②一般工商业用户中的部分小规模的加工业企业,此类用户生产效益低,具有较高的移峰潜力;③居民用户中的部分用户,此类用户节电意识强,对用电成本比较敏感。
(3)从众型。该类用户对电价的响应程度介于顽固型和积极型之间。代表用户包括:① 大工业用户中的食品纺织物加工业、电子设备制造业等,此类用户负荷峰谷分明,具有移峰潜力,但用电成本占生产成本比例不够高;②一般工商业用户中的运输仓储业、批发零售业等,此类用户具有一定的节电意识,但负荷可调节能力较差。
2.2 分时电价作用机理
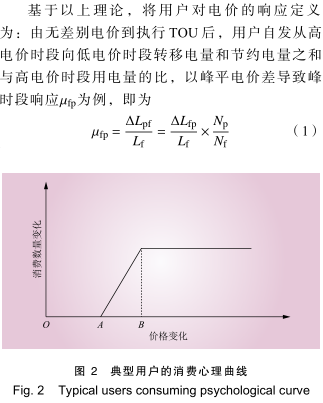
根据消费者心理学原理,用户消费行为受价格变化的影响。为了简化问题,通常将该影响过程抽象为分段线性函数,如图 2 所示。用户对价格的响应有一个差别阈值,当价格变化小于差别阈值,用户对于价格变化几乎没有反应,即原点O 到 A 的区域;当价格变化大于差别阈值时,用户的反应与电价信号的变化程度有关,即线性区AB;用户对价格的响应也会达到一个饱和值,即B 点到正无穷。综上,用户对电价的响应度曲线由该类用户的差别阈值、线性区斜率和饱和值3 个参数确定[12-15]。




3 计及负荷发展的分时电价优化模型
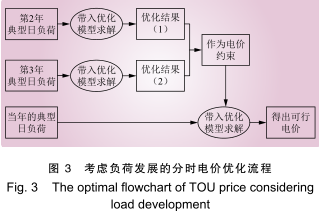
分时电价根据不同的电能价值将用电时间划分为不同时段并制定各时段的电价,在其制定之后的一段时间内不做改变。然而随着时间的推移,电网规模的扩大和行业结构的调整使得负荷曲线形状及用户组成均有所改变,分时电价对用户的刺激逐渐偏离最初期望值。因此,在根据用户响应情况对某地区特定行业进行分时电价优化的过程中,还需要对该地区此行业的未来负荷曲线进行预测,将负荷发展情况计入优化模型。本文在传统的分时电价优化模型的基础上,引入未来两年负荷发展影响因素,利用分时电价优化模型针对预测所得的第 2 年、第 3 年典型日负荷曲线分别计算最优电价,将所得优化结果作为电价约束条件加入到优化模型中,再将当年的典型日负荷曲线带入改进后的优化模型进行计算,所得即为最终的分时电价。考虑负荷发展的分时电价优化流程如图 3 所示。
3.1 典型日负荷曲线预测方法
在考虑电网发展时,需要获得在分时电价实施年限内的未来典型日负荷曲线,即需要根据历史数据预测出未来几年的典型日负荷曲线。对于未来几年典型日负荷曲线的预测具有其特殊性,从时间维度上看属于中长期负荷预测的范畴;但从形式上来看,其本质是用以往的具有一定规律的负荷点,预测未来的负荷点,属于短期负荷预测的范畴 [17] 。本文对典型日负荷曲线采取分解后分别预测再合成的方法,将负荷曲线分解成为表征其发展规律的发展分量和表征其波动规律的波动分量,发展分量取往年的典型日最大负荷,波动分量取该年典型日各点负荷与最大负荷的比值。预测流程如图 4 所示。
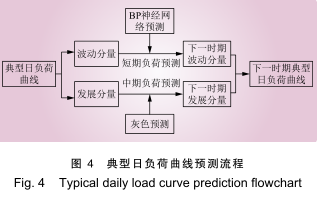
(1)发展分量预测。对于发展分量,本文利用基于灰色 GM(1,1)的中长期负荷预测技术进行预测。灰色理论认为系统的行为现象是朦胧有序的。灰数的生成,就是从杂乱中寻找出规律。同时,灰色理论建立的是生成数据模型,不是原始数据模型,因此,灰色预测的数据是通过生成数据的 GM(1,1)模型所得到的预测值的逆处理结果。
(2)波动分量预测。假设在一定的时间内,各行业用电负荷的波动基本稳定,如此可以利用短期负荷预测技术来得到未来负荷的波动分量。BP 网络是一种按误差逆传播算法训练的多层前馈网络,它通过反向传播来不断调整网络的权值和阈值,使网络的误差平方和最小。该模型拓扑结构包括输入层、隐含层和输出层。本文以历史数据为输入层,输出层即期望得到的波动分量[18-19]。
3.2 目标函数
TOU 优化目标是尽可能削峰填谷,减小系统备用容量,充分利用谷时段电量,从而达到提高系统负荷率、运行效率和稳定性的目的。

3.3 约束条件
3.3.1 电力公司的销售收入不变

3.3.4 峰谷电价比约束
实行 TOU 的目的是使负荷曲线尽量趋于平缓,但若峰谷价差过大,用户的响应行为将过于激烈,甚至可能造成峰谷倒置现象,对电力系统造成新的压力,因此有必要给峰谷电价设置合理的比例,在本文算例中取
1.2
3.3.5 用户购电费用约束
从用户角度考虑,分时电价应能降低用户电费支出。即实行 TOU 后,用户电费的支出不应该大于TOU 实施前用户的支出。由于用户所支出的购电费用即为电力公司的售电收入,故此约束条件可表述为
MTOU≤MNON(18)
3.3.6 用户用电量约束
电价的改变以保证用户的正常用电需求为前提,即实施 TOU 后用户将高电价时段可调节的用电量完全转移到低电价时段,用户的用电量基本保持不变。该约束条件与电力公司售电量保持不变表达式相同,如式(14)所示。
4 算例分析
假设在实施分时电价前,对该地区用户均实行平均电价,大工业为 0.633 元/(kW˙h);一般工商业为 0.829 元/(kW˙h);居民为 0.518 元/(kW˙h)。假设系统在谷时段的运行边际成本 P MaCOST 为 0.27 元/(kW˙h),小发电机组在峰时段的发电成本价 P GeCOST为 1.48 元/(kW˙h)。该地区各用户类型的典型日负荷曲线如图 5所示,分时电价作用机理模型的相关参数设置如表 1 所示。本算例根据大工业、工商业和居民 3 类负荷曲线,采用模糊数学的方法作出分时电价时段划分,其中以偏大型半梯形分布和偏小型半梯形分布作为隶属度函数分别确定各点处于峰时段和谷时段的可能性,划分结果如图 6 所示。根据历史数据采用 4.1 的预测方法得到的第2 年和第 3 年数据,并利用 CPLEX 商业优化软件求解分时电价优化模型,将仅考虑当年典型日负荷曲线优化制定的分时电价(称为“电价一”)与考虑负荷发展而优化制定的分时电价(称为“电价二”)进行对比,结果如表 2 所示。针对第 2 年和第 3 年的负荷情况,用户对表 2 中所列出的不同电价有不同的响应结果。第2 年负荷曲线在不同电价下响应的高峰、低谷时段负荷曲线为图 7 和图 8。第 3 年负荷曲线在不同电价下响应的高峰、低谷时段负荷曲线为图 9和图 10。本文使用了最大/最小负荷、峰谷差率及负荷波动率指标来衡量 3 年负荷在 2 种电价下的响应情况,具体数值如表 3 所示。
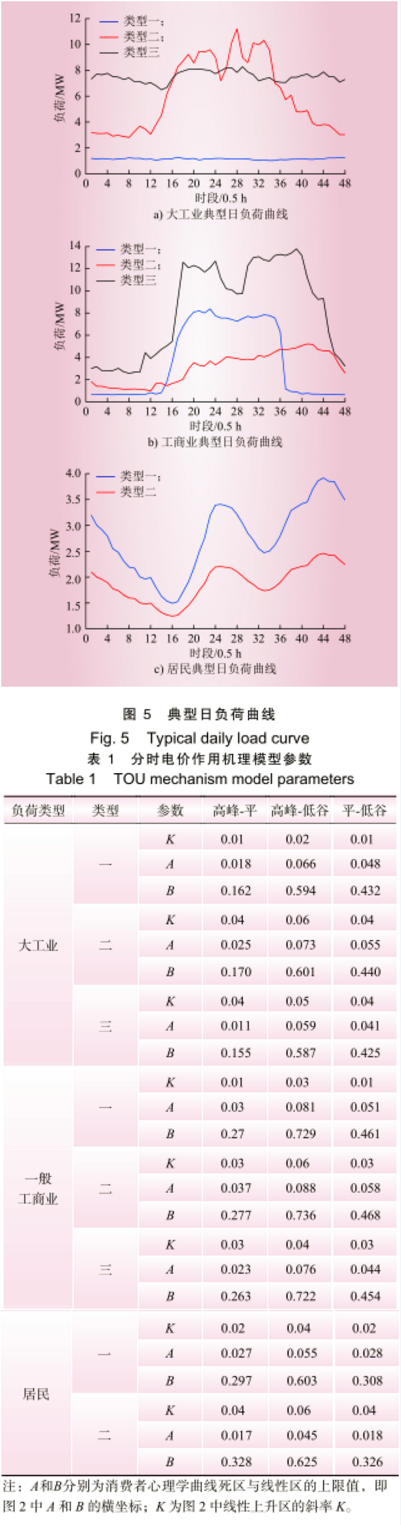
根据实施 2 种电价后的负荷特性,可以发现在实施电价一的情况下,削峰填谷的作用虽然较为明显,但随着时间的推移,削峰作用由第 1 年的 2.523% 减小到第 3 年的 2.262%,平缓负荷波动作用的发展也不尽如人意。然而在实施电价二的情况下,第 2 年和第 3 年的最大负荷较实施电价一时的情况均有所降低,到第 3 年的削峰率比实施电价一增加 0.11%,最小负荷上升,填谷率差距增加至 0.343%,负荷波动率进一步减小,峰谷差率也都有所提高。由此可以得出考虑负荷发展的分时电价优化模型得到的分时电价对未来的负荷适应性较好,在分时电价实行后的第 2 年与第3 年仍可以对用户起到持续性的激励作用。

5 结论
本文针对分时电价对用户的激励效果时效性不足的问题,提出了一种考虑负荷发展的分时电价优化方法。通过算例将仅考虑当年典型日负荷曲线制定的分时电价(电价一)与考虑负荷优化制定的分时电价(电价二)进行对比,得出结果为:(1)在实施电价二的情况下,最大负荷较实施电价一的情况有所降低,最小负荷上升,负荷波动率减小,峰谷差率都有所提高。(2)考虑负荷发展优化得到的分时电价对未来的负荷具有更强的适应性,能在未来时间内刺激用户做出期望的响应。
参考文献:
[1]王冬容. 价格型需求侧响应在美国的应用[J]. 电力需求侧管理,2010, 12(4): 74–77.WANG Dongrong. Application of price-based demand side responsein the U.S.A.[J]. Power Demand Side Management, 2010, 12(4):74–77.
[2]FARUQUI A, GEORGE S S. The value of dynamic pricing in massmarkets[J]. The Electricity Journal, 2002, 15(6): 45–55.
[3]汤玉东, 王明飞, 邹云, 等. 基于 DSM 的分时电价研究[J]. 电力需求侧管理, 2000, 2(3): 14–16,19.
[4]汤玉东, 吴军基, 邹云. 基于 DSM 的分时电价的进一步研究[J]. 继电器, 2002, 30(3): 20–22.TANG Yudong, WU Junji, ZOU Yun. Further research on the TOUrate based on DSM[J]. Relay, 2002, 30(3): 20–22.
[5]周博, 王博, 高松, 等. 基于用户响应的分时电价模型研究[J]. 智能电网, 2016, 4(3): 307–311.ZHOU Bo, WANG Bo, GAO Song, et al. Time-of-use price modelbased on customer response[J]. Smart Grid, 2016, 4(3): 307–311.
[6]孙强. 基于价格型需求响应决策优化模型的应用研究[D]. 北京: 华北电力大学, 2016.
[7]李春燕, 许中, 马智远. 计及用户需求响应的分时电价优化模型[J].电力系统及其自动化学报, 2015, 27(3): 11–16.LI Chunyan, XU Zhong, MA Zhiyuan. Optimal time-of-useelectricity price model considering customer demand response[J].Proceedings of the CSU-EPSA, 2015, 27(3): 11–16.
[8]DARYANIAN B, BOHN R E, TABORS R D. Optimal demand-sideresponse to electricity spot prices for storage-type customers[J]. IEEETransactions on Power Systems, 2002, 4(3): 897–903.
[9]程瑜, 翟娜娜. 基于用户响应的分时电价时段划分[J]. 电力系统自动化, 2012, 36(9): 42–46, 53.CHENG Yu, ZHAI Nana. Electricity price peak and valley periodsdivision based on customer response[J]. Automation of ElectricPower Systems, 2012, 36(9): 42–46, 53.
[10]赵明, 董力, 李孟阳, 等. 基于时段聚类的峰谷电价时段确定方法研究[J]. 电力需求侧管理, 2016, 18(4): 11–17.
[11]ZHAO Ming, DONG Li, LI Mengyang, et al. Periods divisionmethod for peak-valley prices based on clustering algorithm[J].Power Demand Side Management, 2016, 18(4): 11–17.郜璘. 基于用户响应的峰谷分时电价决策优化模型的应用研究[D]. 合肥: 合肥工业大学, 2010.
[12]WOYCHIK E C. Optimizing demand response[J]. Public UtilitiesFortnightly, 2008(5): 52–56.
[13]孔祥玉, 杨群, 穆云飞, 等. 分时电价环境下用户负荷需求响应分析方法[J]. 电力系统及其自动化学报, 2015, 27(10): 75–80.KONG Xiangyu, YANG Qun, MU Yunfei, et al. Analysis method forcustomers demand response in time of using price[J]. Proceedings ofthe CSU-EPSA, 2015, 27(10): 75–80.
[14]刘继东, 韩学山, 韩伟吉, 等. 分时电价下用户响应行为的模型与算法[J]. 电网技术, 2013, 37(10): 2973–2978.LIU Jidong, HAN Xueshan, HAN Weiji, et al. Model and algorithmof customers' responsive behavior under time-of-use price[J]. PowerSystem Technology, 2013, 37(10): 2973–2978.
[15]董军, 张晓虎, 李春雪, 等. 自动需求响应背景下考虑用户满意度的分时电价最优制定策略[J]. 电力自动化设备, 2016, 36(7): 67–73.DONG Jun, ZHANG Xiaohu, LI Chunxue, et al. Optimal TOUpricing strategy considering user satisfaction in automated demandresponse background[J]. Electric Power Automation Equipment,2016, 36(7): 67–73.
[16]阮文骏, 王蓓蓓, 李扬, 等. 峰谷分时电价下的用户响应行为研究[J]. 电网技术, 2012, 36(7): 86–93.RUAN Wenjun, WANG Beibei, LI Yang, et al. Customer responsebehavior in time-of-use price[J]. Power System Technology, 2012,36(7): 86–93.
[17]唐杰明, 刘俊勇, 杨可, 等. 基于灰色模型和最小二乘支持向量机的电力短期负荷组合预测[J]. 电网技术, 2009, 33(3): 63–68.TANG Jieming, LIU Junyong, YANG Ke, et al. Short-term loadcombination foreing by grey model and least square supportvector machine[J]. Power System Technology, 2009, 33(3): 63–68.
[18]隋惠惠. 基于 BP 神经网络的短期电力负荷预测的研究[D]. 哈尔滨: 哈尔滨工业大学, 2015.
[19]QUAIYUM S, YOUSUF I, KHAN S, et al. Artificial neural networkbased short term load foreing of power system[J]. InternationalJournal of Computer Applications, 2013, 16(4): 335–336.
[20]姜勇, 杨雪纯, 王蓓蓓, 等. 计及需求响应不确定性的智能用电双向互动仿真[J]. 电力系统及其自动化学报, 2016, 28(9): 48–55.JIANG Yong, YANG Xuechun, WANG Beibei, et al. Simulation ofsmart power consumption and bilateral interaction unsideringuncertainty of demand response[J]. Proceedings of the CSU-EPSA,2016, 28(9): 48–55.

责任编辑:仁德财
-
深度文章 | 能源互联网环境下的多能需求响应技术
2020-10-23能源互联网,分布式电源,多能互补 -
秒懂:输配电价核定的流程与要义!
2020-09-21电价,输配电价,电力体制改革 -
如何挖潜区县综合能源市场?答案来了:规划先行!
2020-06-16综合能源服务,清洁能源,新能源消纳
-
有话好好说——漫谈售电合同争议
2020-10-12售电合同争议 -
金风科技今年交付量有望全球第一!
2020-06-30金风科技,风电机组,风电市场 -
探索 | 既耗能又可供能的数据中心 打造融合型综合能源系统
2020-06-16综合能源服务,新能源消纳,能源互联网